La proportionnalité en 6ème est une notion clé. Elle prépare les élèves aux concepts mathématiques plus avancés. Un entraînement régulier est essentiel. Les exercices corrigés en ligne offrent un support précieux.
Voici quelques types d'exercices que l'on retrouve fréquemment.
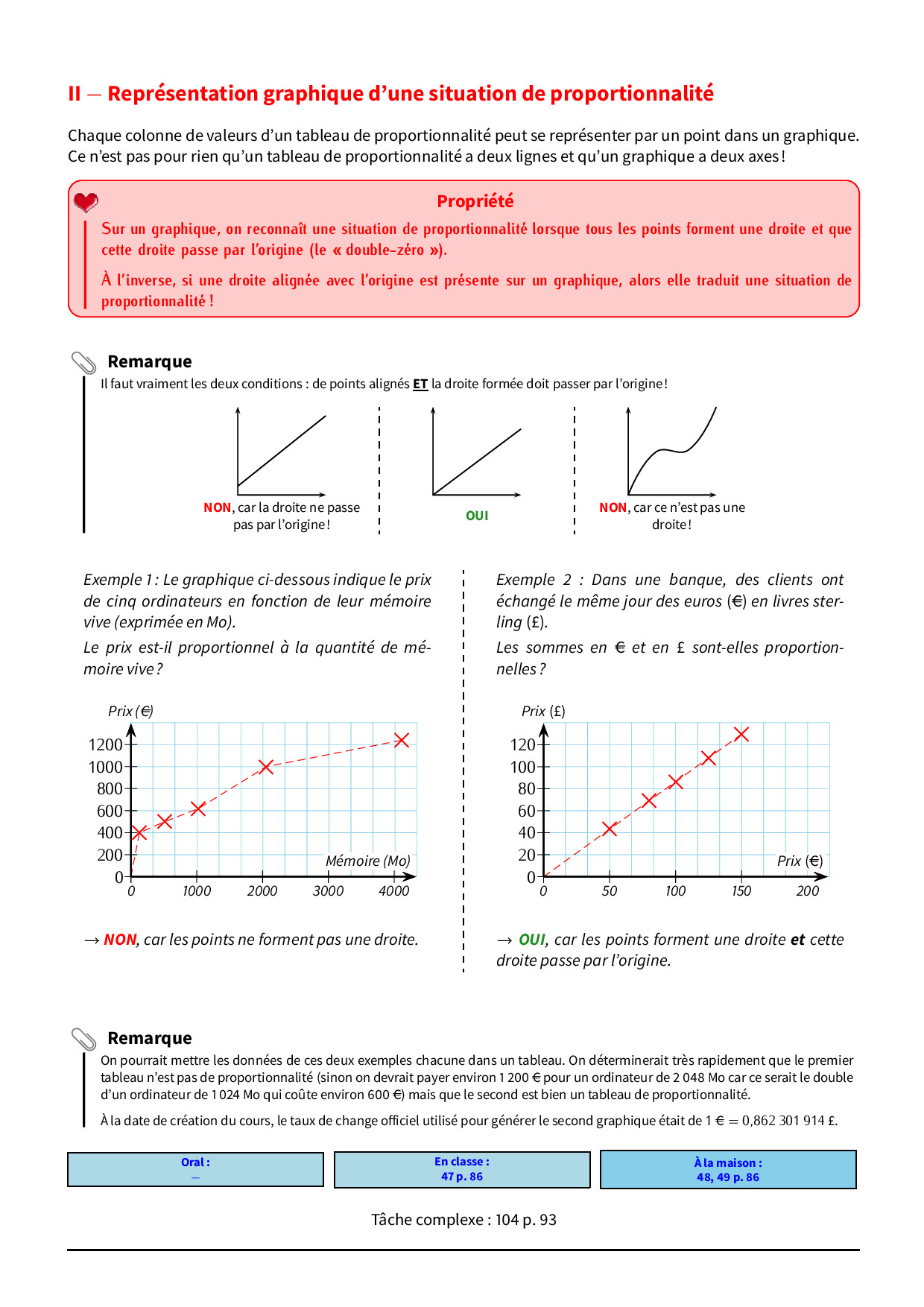
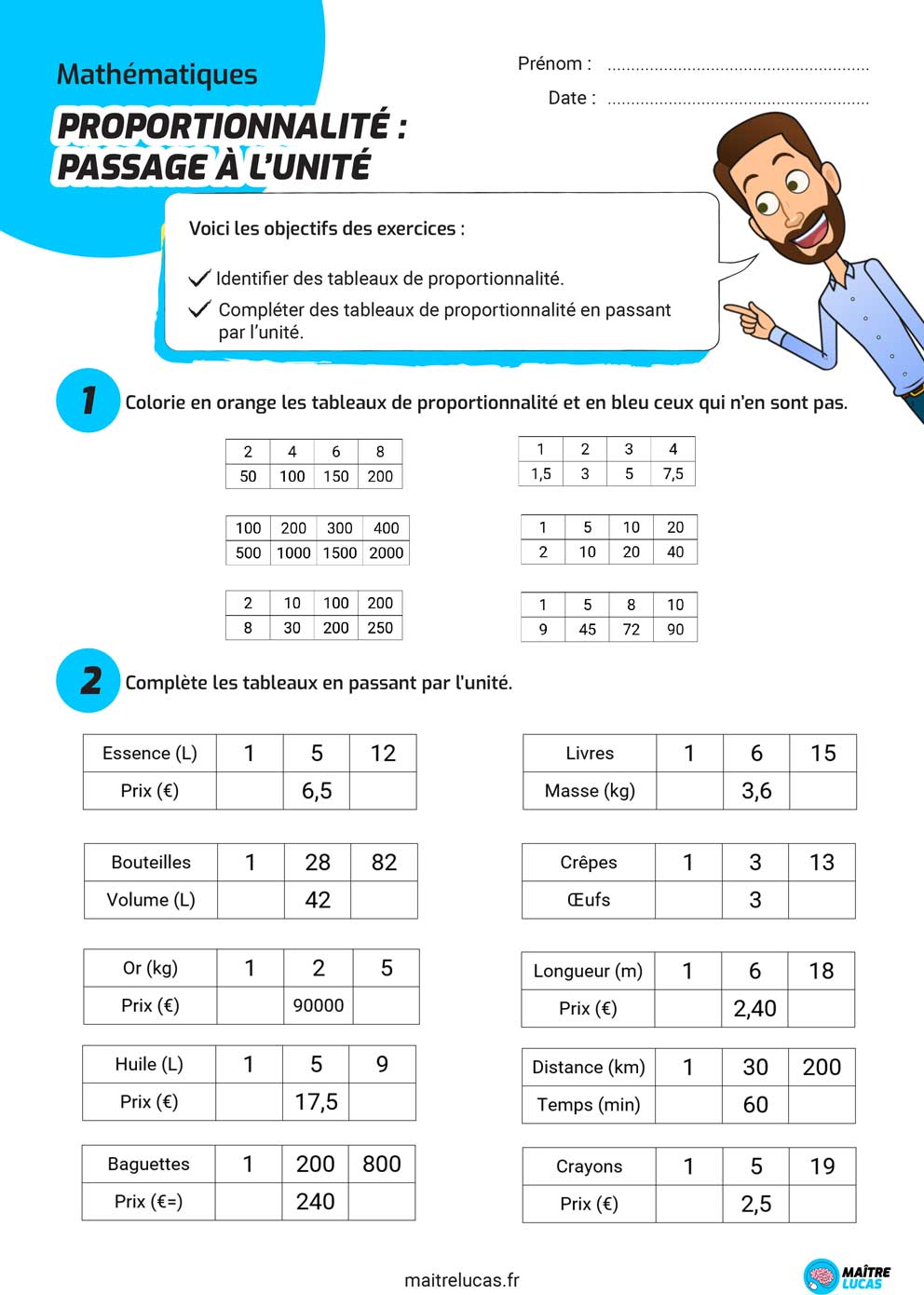
Reconnaître une situation de proportionnalité
Il faut analyser des tableaux. On vérifie si les quotients des valeurs correspondantes sont égaux. Si c'est le cas, c'est une situation de proportionnalité. Sinon, ce n'en est pas une.
Par exemple, un tableau avec le nombre de pommes et leur prix. Si le prix double quand le nombre de pommes double, c'est proportionnel.
Compléter un tableau de proportionnalité
Plusieurs méthodes sont possibles. On peut utiliser le coefficient de proportionnalité. On divise une valeur de la deuxième ligne par la valeur correspondante de la première ligne. Ce résultat est le coefficient. On multiplie ensuite chaque valeur de la première ligne par ce coefficient pour obtenir la valeur correspondante de la deuxième ligne.
Une autre méthode est d'utiliser le produit en croix. Si a/b = c/x, alors x = (b*c)/a. C'est particulièrement utile quand le coefficient de proportionnalité n'est pas évident.
Résoudre des problèmes concrets
Ces problèmes mettent en scène des situations réelles. Par exemple, calculer le prix de plusieurs articles identiques connaissant le prix d'un seul. Ou bien convertir des recettes de cuisine pour un nombre différent de personnes.
La règle de trois est souvent employée. On identifie les grandeurs proportionnelles. On écrit une égalité de fractions. On utilise le produit en croix pour trouver la valeur manquante.
Pourcentages
Calculer un pourcentage d'une quantité est une application directe de la proportionnalité. On transforme le pourcentage en une fraction ou un nombre décimal. On multiplie ensuite cette fraction ou ce nombre par la quantité totale.
Par exemple, calculer 20% de 150. On calcule 20/100 * 150. Ou bien 0,20 * 150.
Échelles
Les échelles sont utilisées sur les cartes et les plans. Elles représentent le rapport entre les dimensions sur le plan et les dimensions réelles. Une échelle de 1/100 signifie que 1 cm sur le plan représente 100 cm dans la réalité.
Pour convertir des distances, on utilise la proportionnalité. Si une distance sur le plan est de 5 cm et l'échelle est de 1/100, la distance réelle est de 5 * 100 = 500 cm, soit 5 mètres.
Vitesse, Distance, Temps
La relation entre la vitesse, la distance et le temps est un exemple classique de proportionnalité. À vitesse constante, la distance parcourue est proportionnelle au temps. La formule est distance = vitesse * temps.
Pour résoudre des problèmes impliquant ces grandeurs, il faut s'assurer que les unités sont cohérentes. Par exemple, si la vitesse est en km/h, le temps doit être en heures et la distance en kilomètres.
Graphiques
Représenter une situation de proportionnalité graphiquement donne une ligne droite passant par l'origine. L'axe des abscisses représente une grandeur. L'axe des ordonnées représente l'autre grandeur.
On place quelques points correspondant à des valeurs connues. On trace ensuite la droite passant par ces points et l'origine. On peut utiliser ce graphique pour déterminer des valeurs inconnues.
Outils en ligne
De nombreux sites web proposent des exercices corrigés. Ils offrent un entraînement personnalisé. Ils permettent de s'exercer à son propre rythme. Les corrections sont souvent détaillées. Elles aident à comprendre les erreurs.
Les exercices interactifs sont particulièrement utiles. Ils permettent de manipuler les données. Ils rendent l'apprentissage plus ludique.
Conseils pour réussir
Lire attentivement l'énoncé. Identifier les informations importantes. Définir les grandeurs proportionnelles. Choisir la méthode appropriée (coefficient de proportionnalité, produit en croix, etc.). Vérifier les résultats.
S'entraîner régulièrement. Ne pas hésiter à demander de l'aide. Comprendre les erreurs. Refaire les exercices.
La proportionnalité est une compétence fondamentale. Elle est utilisée dans de nombreux domaines. Un bon entraînement en 6ème est un atout pour la suite.
Exercices La proportionnalité pour CM1, CM2, 6E - Maître Lucas