Comment Démontrer Que Deux Triangles Sont Semblables

Démontrer la similitude de deux triangles est une compétence fondamentale en géométrie. Plusieurs méthodes rigoureuses permettent d'établir cette relation. Explorons les critères les plus fiables.

Critère AAA (Angle-Angle-Angle)

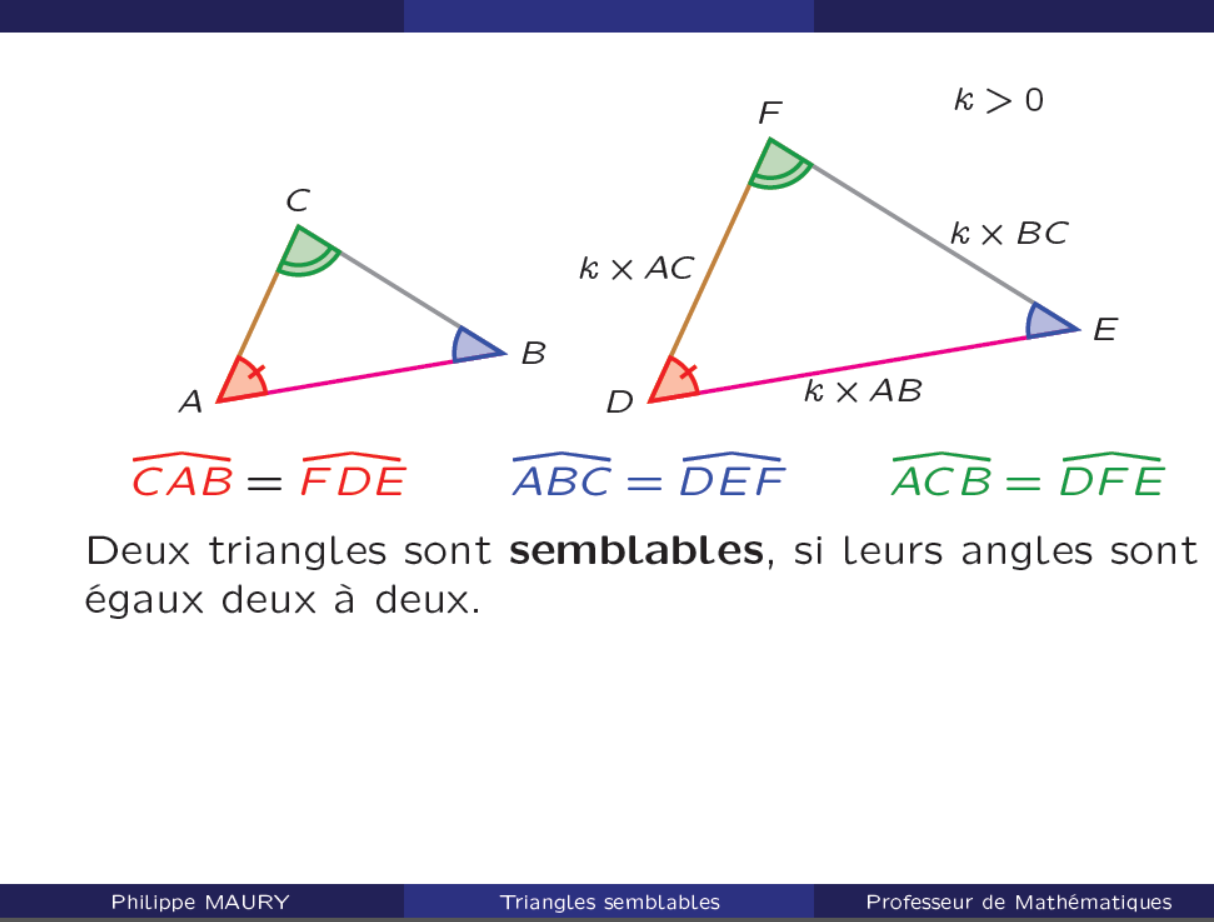
Ce critère est souvent le point de départ. Si deux triangles ont leurs trois angles respectivement égaux, alors ils sont semblables. La démonstration repose sur le fait que la somme des angles d'un triangle est constante (180 degrés). Connaissant deux angles égaux, le troisième l'est forcément.

Vérifiez l'égalité des angles. Utilisez un rapporteur pour mesurer précisément les angles. Une autre méthode consiste à exploiter les propriétés des angles formés par des droites parallèles coupées par une sécante.

Critère AA (Angle-Angle)

En réalité, le critère AAA est souvent simplifié. Il suffit de démontrer que deux angles d'un triangle sont respectivement égaux à deux angles d'un autre triangle. Le troisième angle sera alors automatiquement égal. La similitude est alors établie.

Cette simplification est essentielle. Elle permet une démonstration plus rapide. Recherchez donc en priorité deux paires d'angles égaux.

Critère SSS (Side-Side-Side)

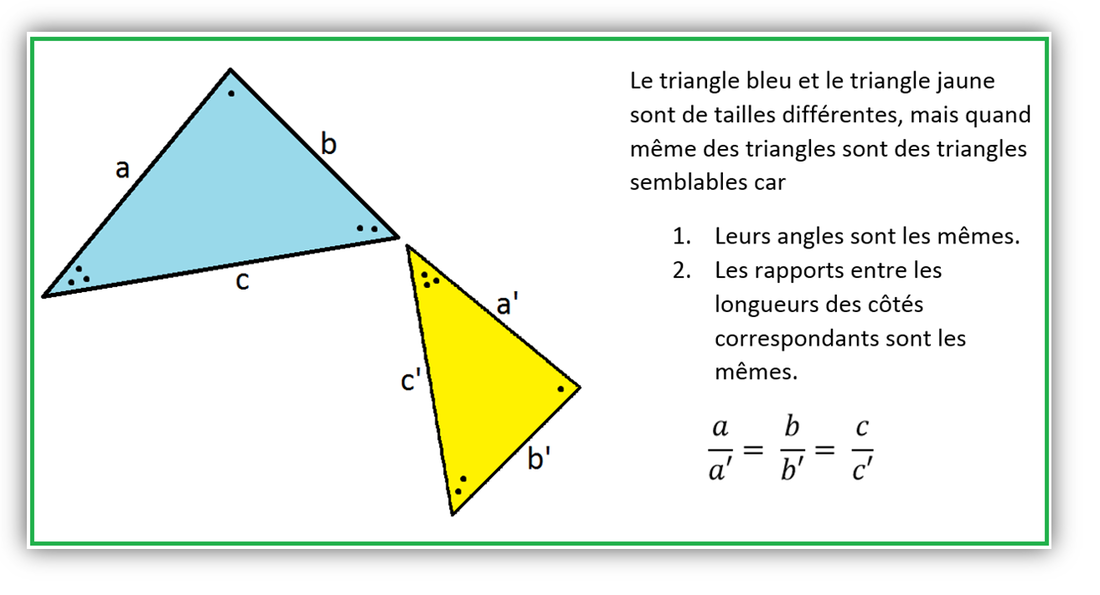
Ce critère s'intéresse aux longueurs des côtés. Si les longueurs des trois côtés d'un triangle sont proportionnelles aux longueurs des trois côtés d'un autre triangle, alors les deux triangles sont semblables.

Calculez les rapports des côtés correspondants. Vérifiez que ces rapports sont égaux. Une attention particulière doit être portée à l'identification des côtés correspondants. Ce sont ceux qui sont opposés aux angles égaux (ou supposés égaux).

Critère SAS (Side-Angle-Side)

Ce critère combine les longueurs des côtés et la mesure d'un angle. Si deux côtés d'un triangle sont proportionnels à deux côtés d'un autre triangle, et si l'angle compris entre ces côtés est égal dans les deux triangles, alors les deux triangles sont semblables.

Identifiez l'angle compris entre les deux côtés considérés. Mesurez cet angle avec précision. Calculez les rapports des longueurs des côtés concernés. Assurez-vous que l'égalité de l'angle et la proportionnalité des côtés sont vérifiées simultanément.

Critère ASA (Angle-Side-Angle)

Ce critère se concentre sur un côté et les deux angles adjacents. Si deux angles d'un triangle sont respectivement égaux à deux angles d'un autre triangle, et si le côté compris entre ces angles a une longueur proportionnelle aux côtés homologues, alors les deux triangles sont semblables.

Repérez le côté compris entre les deux angles considérés. Mesurez les angles adjacents avec précision. Calculez le rapport des longueurs des côtés concernés. Ce critère est particulièrement utile lorsque l'on connaît peu d'informations sur les autres côtés.

Théorème de Thalès

Le théorème de Thalès est un outil puissant pour démontrer la similitude de triangles. Il s'applique lorsque deux droites sont coupées par des droites parallèles. Il stipule que les triangles formés sont semblables.

Identifiez les droites parallèles et les droites sécantes. Appliquez le théorème de Thalès pour établir la proportionnalité des côtés. Déduisez-en la similitude des triangles.

Exemple Concret

Supposons deux triangles, ABC et DEF. On sait que l'angle A est égal à l'angle D, et que l'angle B est égal à l'angle E. D'après le critère AA, les triangles ABC et DEF sont semblables.

Autre exemple : On a les longueurs suivantes : AB = 4, BC = 6, CA = 8 et DE = 2, EF = 3, FD = 4. On calcule les rapports : AB/DE = 4/2 = 2, BC/EF = 6/3 = 2, CA/FD = 8/4 = 2. Tous les rapports sont égaux à 2. D'après le critère SSS, les triangles ABC et DEF sont semblables.

Précautions et Remarques

L'ordre des sommets est crucial lors de l'énoncé de la similitude. Assurez-vous de respecter la correspondance des angles et des côtés. Une notation correcte est essentielle pour éviter les erreurs d'interprétation.

La congruence est un cas particulier de similitude. Deux triangles congruents sont semblables, avec un rapport de similitude égal à 1. La congruence implique une égalité parfaite des formes et des dimensions.

La maîtrise de ces critères et théorèmes est indispensable pour résoudre des problèmes de géométrie complexes. Une pratique régulière est essentielle pour acquérir une solide compréhension de ces concepts. Une visualisation claire des figures est également un atout précieux.