Patron Pyramide à Base Rectangulaire Mathématiques 4ème

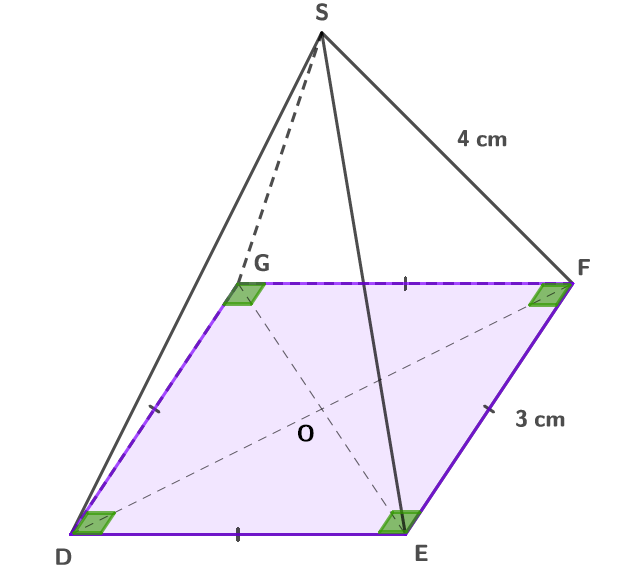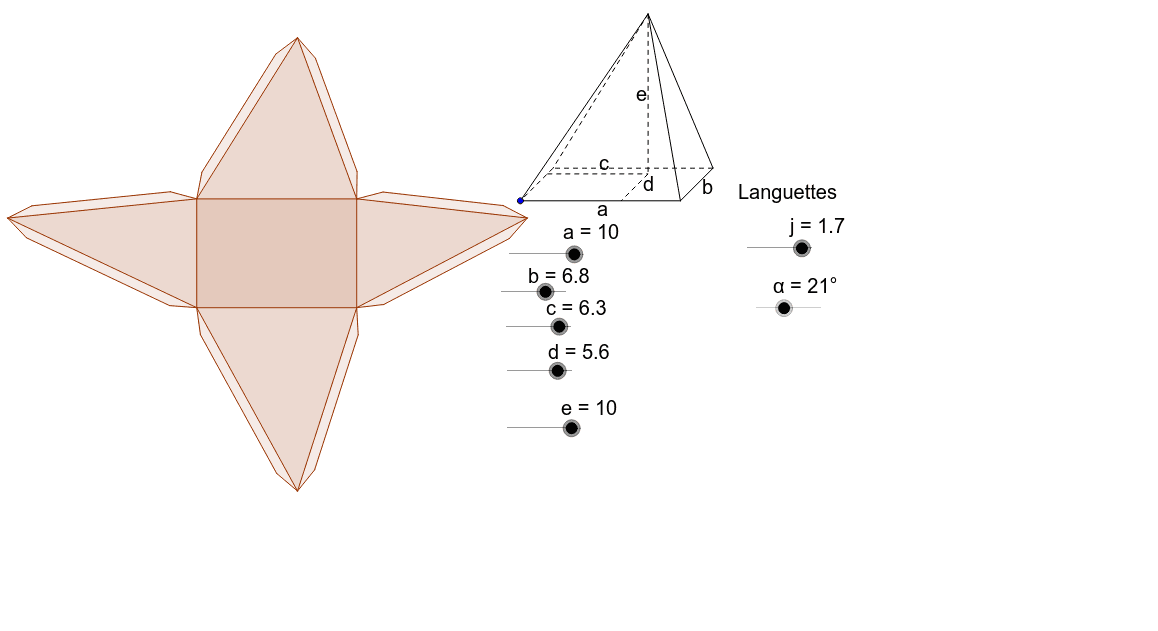
Voici le patron d'une pyramide à base rectangulaire, une exploration géométrique précise et exhaustive.

L'élément fondamental de cette pyramide est son rectangle de base. Ses dimensions, longueur (L) et largeur (l), sont primordiales.

Le patron requiert la définition précise de ces dimensions. Une mesure exacte est impérative.

Quatre triangles isocèles ou scalènes se dressent à partir de chaque côté du rectangle. Ces triangles composent les faces latérales.

Construction des Triangles Latéraux

Le premier triangle, adossé à la longueur L, possède une hauteur spécifique (h1). Cette hauteur détermine l'inclinaison de cette face.

Le second triangle, également adossé à la longueur L, peut avoir une hauteur différente (h2). L'asymétrie est possible.

Le troisième triangle, lié à la largeur l, présente une hauteur (h3) influençant l'aspect de la pyramide.

Le quatrième triangle, s'appuyant sur la largeur l, affiche une hauteur (h4). Cette hauteur peut différer de h3.

La précision des hauteurs est cruciale. Des mesures incorrectes altèrent la forme finale.

Assemblage du Patron

Le patron se construit en attachant chaque triangle à son côté correspondant du rectangle. Une disposition rigoureuse est indispensable.

Des languettes de collage, discrètement positionnées, facilitent l'assemblage. Elles assurent une jonction propre et solide.

Ces languettes, intégrées aux bords des triangles et du rectangle, sont essentielles. Leur largeur doit être minimale pour une discrétion optimale.

Le pliage des triangles s'effectue le long des arêtes. L'angle de pliage est déterminé par les dimensions du rectangle et les hauteurs des triangles.

Calculs Essentiels

L'aire de la base rectangulaire se calcule simplement : Aire = L x l. Cette valeur est un point de départ.

L'aire de chaque triangle se calcule comme suit : (Base x Hauteur) / 2. L'addition de ces aires est nécessaire.

L'aire totale de la pyramide est la somme de l'aire de la base et des aires des quatre triangles.

Le volume de la pyramide se calcule par la formule : (1/3) x Aire de la base x Hauteur de la pyramide (H). H représente la distance perpendiculaire du sommet au plan de la base. La hauteur H n'est pas directement visible sur le patron, mais se calcule à partir des hauteurs des faces latérales et des dimensions de la base.

Représentation du Patron

Le patron doit être représenté à l'échelle. Une échelle appropriée permet une construction précise.

L'utilisation d'un logiciel de dessin assisté par ordinateur (DAO) est recommandée. La précision est ainsi optimisée.

Les lignes de pliage doivent être clairement indiquées. Un trait pointillé est souvent utilisé.

Les languettes de collage sont différenciées par une couleur distincte. Cela simplifie l'identification lors de l'assemblage.

Variations et Complexités

La pyramide peut être tronquée. Un plan parallèle à la base coupe la pyramide, créant une base supérieure.

Le patron d'une pyramide tronquée inclut deux rectangles (ou carrés) et quatre trapèzes.

Les calculs d'aire et de volume deviennent plus complexes pour une pyramide tronquée. Des formules spécifiques sont requises.

Les angles des faces latérales peuvent varier considérablement. Une modélisation 3D est alors utile pour visualiser le résultat.

L'orientation de la pyramide dans l'espace affecte la projection du patron. Une rotation est souvent nécessaire.

Matériaux et Techniques

Le papier cartonné est un matériau idéal pour la construction. Sa rigidité assure une bonne tenue.

Le découpage doit être précis et net. L'utilisation d'un cutter est recommandée.

La colle forte est essentielle pour un assemblage durable. Une application minutieuse est nécessaire.

Un pliage soigné garantit une forme pyramidale parfaite. L'utilisation d'une règle facilite le pliage.

Applications

La construction d'un patron de pyramide est un excellent exercice de géométrie. Il permet de visualiser les formes en trois dimensions.

Les pyramides sont utilisées en architecture, en design et en modélisme. Leur forme est esthétiquement plaisante.

La compréhension du patron est fondamentale pour le calcul des aires et des volumes. Ces calculs sont utiles dans de nombreux domaines scientifiques.

Le patron sert de base à la création de maquettes. Il permet de reproduire des objets à petite échelle.

La décomposition d'un solide en un patron simplifie son étude. Cela facilite la compréhension de sa structure.

Conclusion

La maîtrise du patron de pyramide à base rectangulaire est un atout précieux. Elle ouvre la voie à une exploration plus approfondie de la géométrie spatiale. Une représentation rigoureuse et une construction soignée garantissent un résultat optimal. L'étude attentive des dimensions, des hauteurs et des angles est impérative.