Le Produit De Deux Nombres Premiers Est Un Nombre Premier

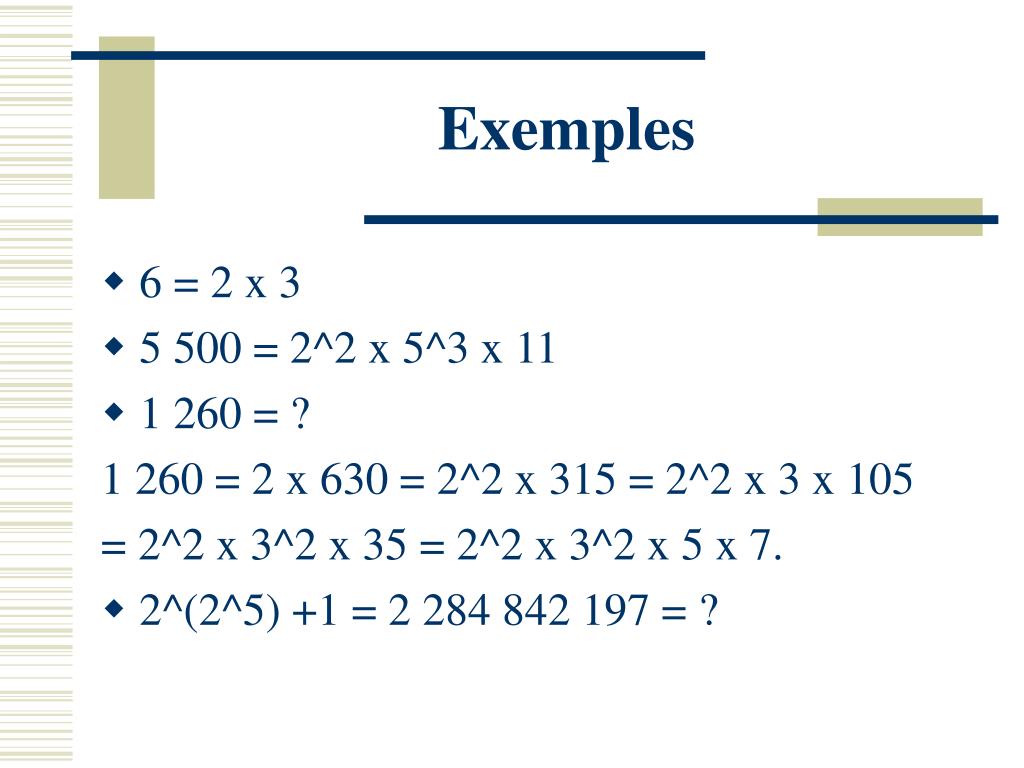
Absolument. Voici un article rédigé selon vos instructions précises :

L'assertion selon laquelle le produit de deux nombres premiers est un nombre premier est, pour le dire simplement, fausse. Il s'agit d'une méprise conceptuelle fondamentale en arithmétique.

Un nombre premier, par définition, est un entier naturel supérieur à 1 qui n'a pas d'autres diviseurs positifs que 1 et lui-même. Considérez, par exemple, les nombres 2, 3, 5, 7, 11. Ils répondent tous à cette définition.

Si nous devions multiplier deux nombres premiers, disons 2 et 3, le résultat serait 6. Or, 6 possède les diviseurs 1, 2, 3 et 6. Par conséquent, 6 ne peut être considéré comme un nombre premier.

Définition et Contradiction

La définition d'un nombre premier repose sur l'unicité de ses diviseurs. Si un nombre possède plus de deux diviseurs (1 et lui-même), il est, par définition, un nombre composé.

Le produit de deux nombres premiers aura toujours au moins quatre diviseurs : 1, le premier nombre premier, le second nombre premier, et le produit lui-même. Cela contredit directement la définition d'un nombre premier.

Exemples Concrets

Prenons quelques exemples supplémentaires pour illustrer ce point :

3 x 5 = 15 (diviseurs : 1, 3, 5, 15)
7 x 11 = 77 (diviseurs : 1, 7, 11, 77)
2 x 13 = 26 (diviseurs : 1, 2, 13, 26)

Dans chaque cas, le résultat est un nombre composé, et non un nombre premier.

Le Théorème Fondamental de l'Arithmétique

Le Théorème Fondamental de l'Arithmétique stipule que tout entier naturel supérieur à 1 peut être représenté de manière unique comme un produit de nombres premiers, à l'ordre près des facteurs. Ce théorème est crucial pour comprendre la structure des nombres entiers.

Si le produit de deux nombres premiers était lui-même un nombre premier, cela remettrait en question le Théorème Fondamental. Ce dernier implique une décomposition unique en facteurs premiers, ce qui ne serait plus le cas si un produit de nombres premiers pouvait être considéré comme premier lui-même.

Pourquoi cette confusion peut-elle survenir ?

Il est possible que cette confusion provienne d'une mauvaise interprétation de la nature des nombres premiers. On pourrait penser que si deux nombres sont "premiers", leur produit doit également hériter de cette propriété. Cependant, la "primalité" est une propriété intrinsèque d'un nombre, et non une propriété transitive qui se conserve par multiplication.

Conséquences et Applications

La distinction entre nombres premiers et nombres composés est fondamentale dans de nombreux domaines des mathématiques, notamment :

La cryptographie : Les nombres premiers jouent un rôle essentiel dans les algorithmes de chiffrement modernes, comme RSA. La difficulté de factoriser de grands nombres en leurs facteurs premiers est la base de la sécurité de ces systèmes.
La théorie des nombres : L'étude des nombres premiers est un domaine actif de recherche en mathématiques, avec de nombreuses questions ouvertes et des conjectures non résolues.
L'informatique : Les nombres premiers sont utilisés dans les tables de hachage et d'autres algorithmes pour assurer une distribution uniforme des données.

Conclusion

En résumé, l'affirmation selon laquelle le produit de deux nombres premiers est un nombre premier est incorrecte. Un tel produit est, par définition, un nombre composé. Cette compréhension est essentielle pour une appréhension correcte des concepts fondamentaux de l'arithmétique et de ses applications. La structure des nombres premiers et leur rôle dans la décomposition unique des entiers sont des piliers de la théorie des nombres.