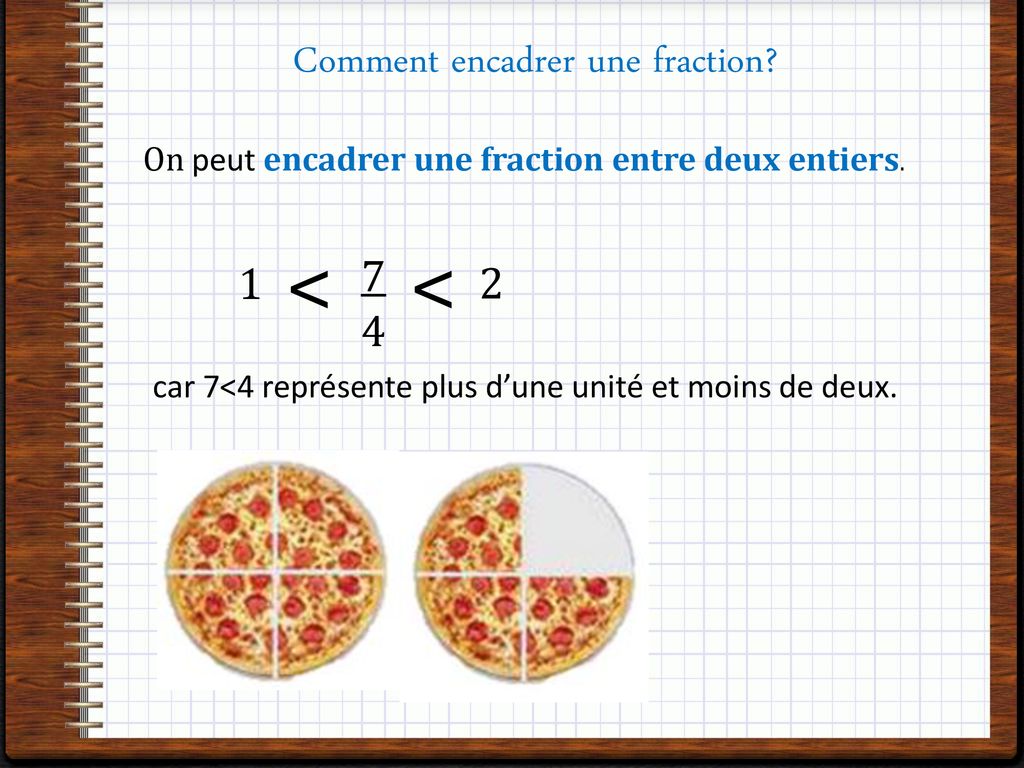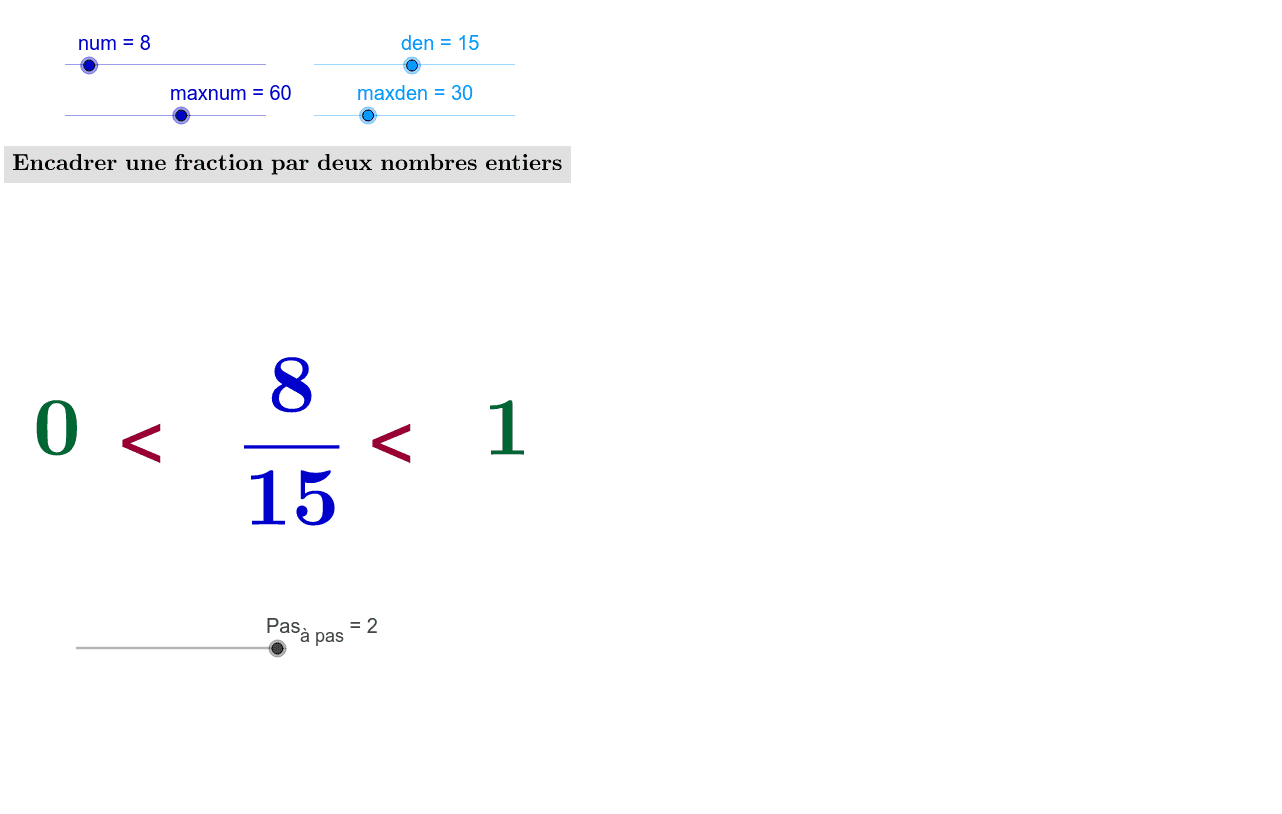
Commençons par les bases. Une fraction, c'est une portion d'un tout. Encadrer, c'est trouver deux nombres entiers qui la serrent de près, un en dessous, l'autre au dessus.
Pour une fraction simple, comme 5/3, divisez 5 par 3. Le résultat est 1,666...
L'entier inférieur est 1. L'entier supérieur est 2. Donc, 1 < 5/3 < 2.
Prenons un autre exemple: 11/4. 11 divisé par 4 donne 2,75.
L'entier inférieur est 2. L'entier supérieur est 3. Ainsi, 2 < 11/4 < 3.
Considérons maintenant une fraction impropre, comme 23/7. La division de 23 par 7 donne environ 3,28.
L'entier inférieur est 3. L'entier supérieur est 4. Donc, 3 < 23/7 < 4.
Quand la fraction est négative, les choses s'inversent. Prenons -7/2. -7 divisé par 2 donne -3,5.
L'entier inférieur est -4. L'entier supérieur est -3. Par conséquent, -4 < -7/2 < -3.
Pour -15/8, la division donne -1,875.
L'entier inférieur est -2. L'entier supérieur est -1. Donc, -2 < -15/8 < -1.
Fractions et Nombres Mixtes
Une fraction peut être exprimée sous forme de nombre mixte. Par exemple, 17/5 peut s'écrire 3 2/5. Le 3 indique l'entier inférieur. L'entier supérieur est 4. Donc, 3 < 17/5 < 4.
Considérons 25/6. Cela donne 4 1/6. L'entier inférieur est 4. L'entier supérieur est 5. Ainsi, 4 < 25/6 < 5.
Pour une fraction comme 31/9, on obtient 3 4/9. L'entier inférieur est 3. L'entier supérieur est 4. Par conséquent, 3 < 31/9 < 4.
Fractions avec Grands Nombres
Si la fraction a de grands nombres, comme 145/12, divisez 145 par 12. Le résultat est 12,0833...
L'entier inférieur est 12. L'entier supérieur est 13. Donc, 12 < 145/12 < 13.
Prenons 278/23. La division donne environ 12,0869...
L'entier inférieur est 12. L'entier supérieur est 13. Ainsi, 12 < 278/23 < 13.
Si on a 567/45, la division donne 12,6.
L'entier inférieur est 12. L'entier supérieur est 13. Par conséquent, 12 < 567/45 < 13.
Cas Particuliers
Si la fraction est égale à un entier, par exemple 6/3 = 2, alors l'encadrement est 2 ≤ 6/3 ≤ 2. On utilise le signe "inférieur ou égal à".
Si la fraction est 9/3 = 3, alors 3 ≤ 9/3 ≤ 3.
Dans le cas de 12/4 = 3, on a 3 ≤ 12/4 ≤ 3.
Fractions et Simplification
Simplifier une fraction avant d'encadrer peut faciliter le travail. Prenons 18/6. On peut simplifier à 3/1 = 3.
Donc, 3 ≤ 18/6 ≤ 3.
Considérons 24/8. Cela se simplifie en 3/1 = 3.
Ainsi, 3 ≤ 24/8 ≤ 3.
Pour 36/12, on obtient 3/1 = 3.
Par conséquent, 3 ≤ 36/12 ≤ 3.
Finalement, n'oubliez pas que l'encadrement est un outil pour comprendre la valeur d'une fraction. La division est la clé. L'observation des nombres entiers qui entourent le résultat de la division permet de déterminer l'encadrement correct. L'entraînement rendra cette opération plus rapide et intuitive.
encadrer une fraction simple par deux entiers consécutifs leçon
-
exercice encadrer fraction entre deux entiers consécutifs
-
exercice encadrer fraction entre deux entiers consécutifs cm1
-
exercice encadrer fraction entre deux entiers consécutifs cm2
-
exercice encadrer une fraction entre deux entiers cm1