Evaluation Angles Et Parallélisme 5ème Avec Correction

En cinquième, la maîtrise des angles et du parallélisme est cruciale. Elle pose les bases de la géométrie. L'évaluation rigoureuse de ces concepts est donc primordiale. Cet article offre une approche détaillée et corrigée pour aborder cette évaluation.

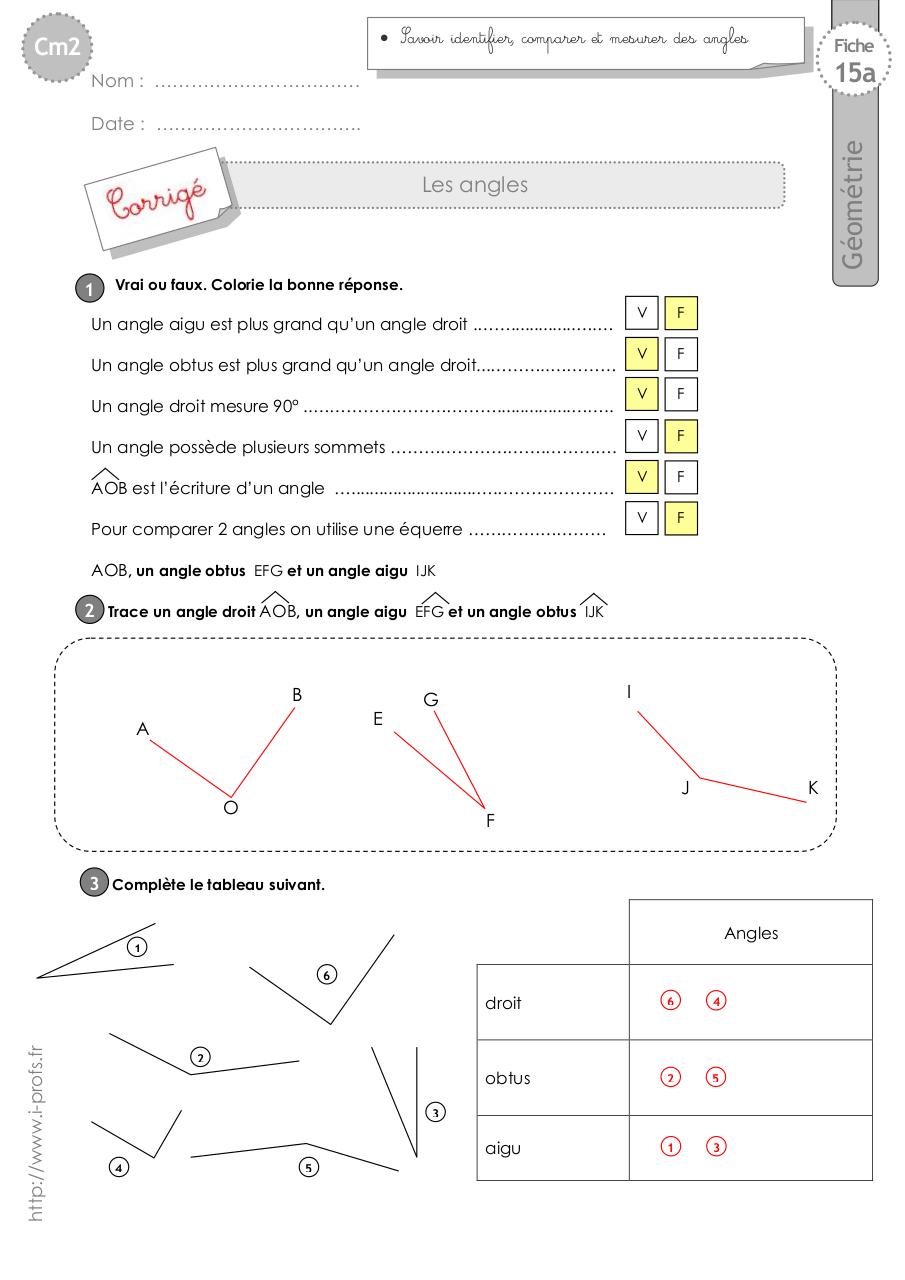
Reconnaître et Nommer les Angles

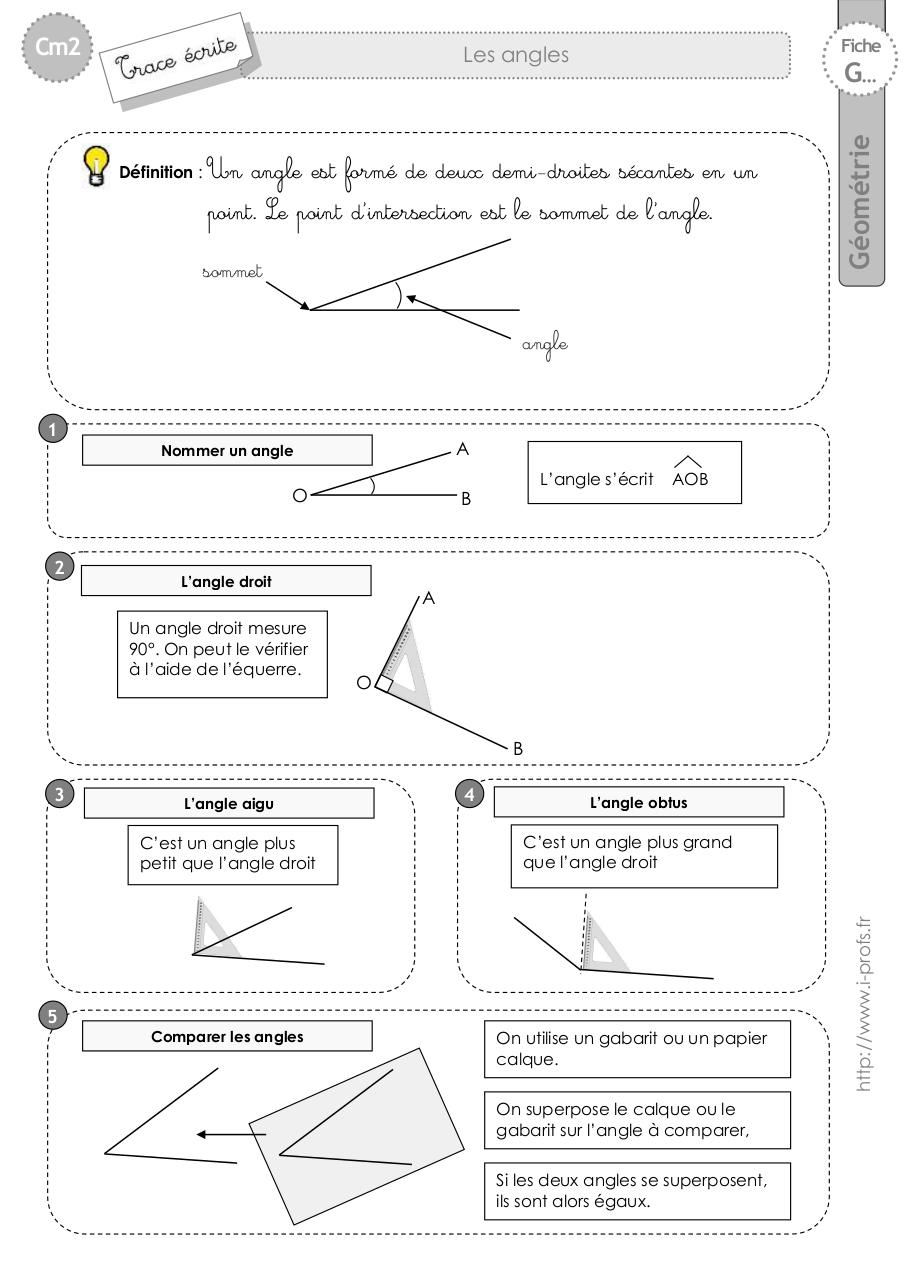
Un angle est formé par deux demi-droites ayant la même origine. Cette origine est le sommet de l'angle. Les deux demi-droites sont les côtés de l'angle.

On nomme un angle avec trois lettres. La lettre du milieu correspond au sommet. On peut aussi le nommer avec une seule lettre, celle du sommet. L'unité de mesure d'un angle est le degré (°).

Types d'Angles

Angle aigu: Sa mesure est comprise entre 0° et 90°.
Angle droit: Sa mesure est exactement 90°.
Angle obtus: Sa mesure est comprise entre 90° et 180°.
Angle plat: Sa mesure est exactement 180°.
Angle rentrant: Sa mesure est comprise entre 180° et 360°.
Angle plein: Sa mesure est exactement 360°.

Angles Complémentaires et Supplémentaires

Deux angles sont complémentaires si la somme de leurs mesures est égale à 90°. Deux angles sont supplémentaires si la somme de leurs mesures est égale à 180°.

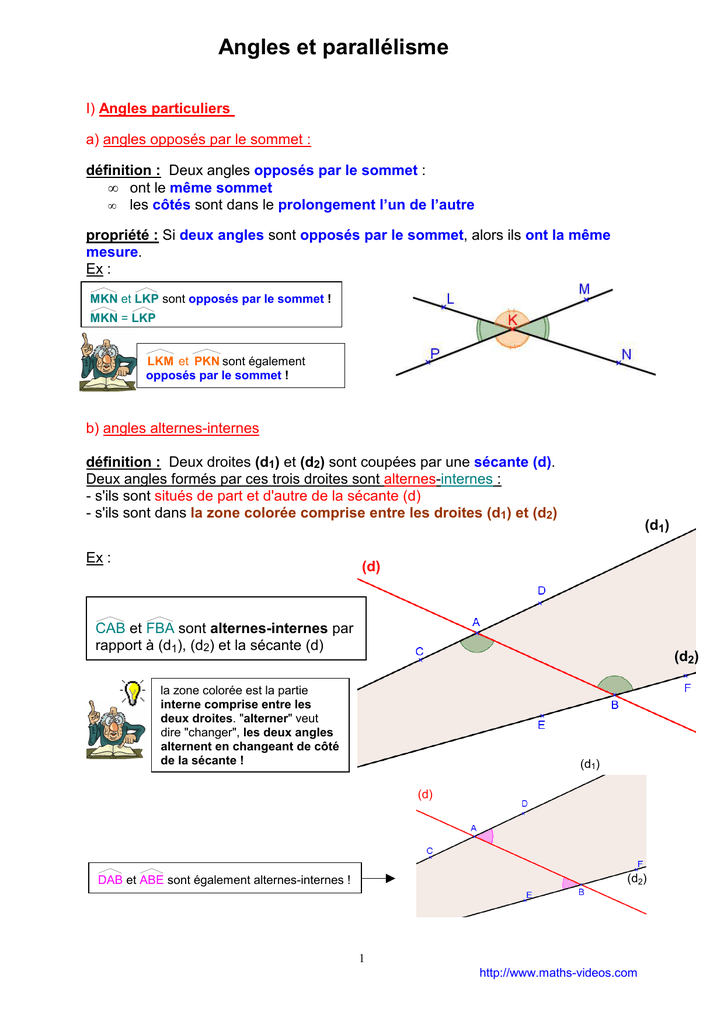
Angles Opposés par le Sommet

Deux angles opposés par le sommet ont le même sommet. Leurs côtés sont le prolongement l'un de l'autre. Ils ont la même mesure.

Droites Parallèles et Sécantes

Deux droites sont parallèles si elles ne se coupent jamais. Une sécante est une droite qui coupe deux ou plusieurs autres droites.

Angles Formés par une Sécante et Deux Parallèles

Lorsqu'une sécante coupe deux droites parallèles, elle forme des paires d'angles spécifiques.

Angles alternes-internes: Ils sont situés de part et d'autre de la sécante, à l'intérieur des deux parallèles. Ils ont la même mesure.
Angles alternes-externes: Ils sont situés de part et d'autre de la sécante, à l'extérieur des deux parallèles. Ils ont la même mesure.
Angles correspondants: Ils sont situés du même côté de la sécante. L'un est à l'intérieur des parallèles et l'autre à l'extérieur. Ils ont la même mesure.

Exercices d'Évaluation et Corrections

Exercice 1:

Soient deux droites parallèles (d1) et (d2) coupées par une sécante (s). Un angle alterne-interne mesure 65°. Quelle est la mesure de l'autre angle alterne-interne ? Quelle est la mesure de l'angle correspondant ? Quelle est la mesure d'un angle supplémentaire à l'angle de 65° ?

Correction:

L'autre angle alterne-interne mesure 65°.
L'angle correspondant mesure 65°.
L'angle supplémentaire mesure 180° - 65° = 115°.

Exercice 2:

Deux angles sont complémentaires. L'un mesure 32°. Quelle est la mesure de l'autre angle ?

Correction:

L'autre angle mesure 90° - 32° = 58°.

Exercice 3:

Identifiez les types d'angles suivants: 45°, 90°, 120°, 180°.

Correction:

45°: Angle aigu.
90°: Angle droit.
120°: Angle obtus.
180°: Angle plat.

Exercice 4:

Dans la figure ci-dessous, les droites (AB) et (CD) sont-elles parallèles ? Justifiez votre réponse. On vous donne: l'angle BAC = 70° et l'angle ACD = 110°.

Correction:

Non, les droites (AB) et (CD) ne sont pas parallèles. Si elles l'étaient, les angles BAC et ACD seraient supplémentaires (car ils formeraient une paire d'angles internes du même côté de la sécante). Or, 70° + 110° = 180°, ce qui montre que l'angle ACD n'est pas supplementaire de BAC, donc elle ne sont pas parallèles.

Exercice 5:

Dessinez deux droites parallèles coupées par une sécante. Marquez un angle de 50°. Déterminez la mesure de tous les autres angles formés.

Correction:

L'angle opposé par le sommet à l'angle de 50° mesure 50°.
Les angles alternes-internes et alternes-externes à l'angle de 50° mesurent également 50°.
Les angles supplémentaires à l'angle de 50° mesurent 180° - 50° = 130°. Leurs angles opposés par le sommet, alternes-internes et alternes-externes mesurent également 130°.

Conseils pour l'Évaluation

Utiliser une variété d'exercices (identification, calculs, démonstrations).
Proposer des figures géométriques claires et précises.
Vérifier la compréhension des définitions et des propriétés.
Encourager les élèves à justifier leurs réponses.
Fournir un feedback constructif pour favoriser la progression.

Conclusion

L'évaluation des angles et du parallélisme en cinquième nécessite une approche méthodique. Les exercices proposés, accompagnés de leurs corrections détaillées, offrent un outil précieux pour évaluer la compréhension des élèves et identifier les points à renforcer. La maîtrise de ces notions est essentielle pour la suite de leur parcours en géométrie.