Comment Calculer La Hauteur D'un Triangle Quelconque

Calculer la hauteur d'un triangle quelconque est une compétence fondamentale en géométrie. Plusieurs méthodes existent. Elles dépendent des informations disponibles sur le triangle.

Méthode 1: Aire et Base Connue

Si l'aire (A) et la longueur d'une base (b) sont connues, la hauteur (h) se calcule par la formule :

h = 2A / b

Par exemple, si l'aire d'un triangle est de 20 cm² et que la base mesure 5 cm, alors la hauteur est:

h = 2 * 20 / 5 = 8 cm.

Méthode 2: Trigonométrie

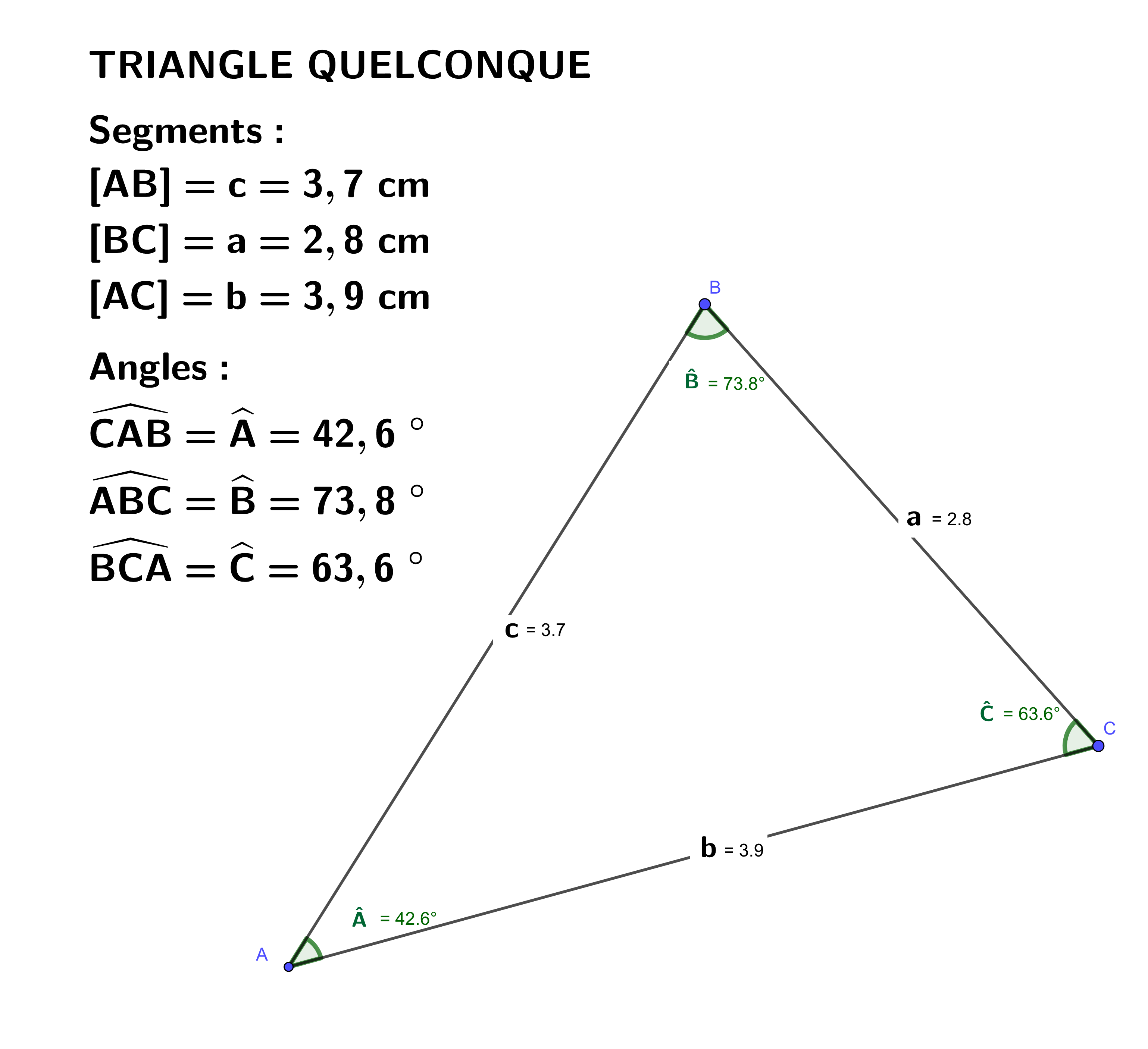
Si un angle et la longueur d'un côté adjacent à cet angle sont connus, on peut utiliser la trigonométrie. Supposons que vous connaissez l'angle α et la longueur du côté c adjacent à l'angle α. La hauteur h relative à la base adjacente à cet angle se calcule comme suit :

h = c * sin(α)

Par exemple, si l'angle α est de 30 degrés et que le côté c mesure 10 cm, alors :

h = 10 * sin(30°) = 10 * 0.5 = 5 cm.

Si vous connaissez l'angle β opposé à la hauteur et la longueur du côté opposé à cet angle (a), la hauteur se calcule directement :

h = a * sin(β)

Méthode 3: Formule de Héron

Si vous connaissez les longueurs des trois côtés (a, b, c) du triangle, vous pouvez calculer la hauteur en utilisant la formule de Héron pour calculer l'aire. La formule de Héron est :

A = √(s(s-a)(s-b)(s-c))

où s est le demi-périmètre du triangle:

s = (a + b + c) / 2

Une fois l'aire A calculée, vous pouvez utiliser la formule de la première méthode (h = 2A / b) pour trouver la hauteur. Choisissez n'importe quel côté comme base (b).

Par exemple, si a = 5 cm, b = 6 cm, et c = 7 cm, alors :

s = (5 + 6 + 7) / 2 = 9 cm

A = √(9(9-5)(9-6)(9-7)) = √(9 * 4 * 3 * 2) = √216 ≈ 14.7 cm²

Si nous choisissons b = 6 cm comme base, alors :

h = 2 * 14.7 / 6 = 4.9 cm.

Méthode 4: Coordonnées des Sommets

Si vous connaissez les coordonnées des sommets du triangle dans un plan cartésien, vous pouvez utiliser la formule de la distance entre un point et une droite. Soient les sommets A(x1, y1), B(x2, y2), et C(x3, y3). Supposons que vous voulez trouver la hauteur issue du sommet C sur la base AB.

Déterminez l'équation de la droite AB. La pente (m) de la droite AB est :

m = (y2 - y1) / (x2 - x1)

L'équation de la droite AB est alors :

y - y1 = m(x - x1)

Que l'on peut réécrire sous la forme ax + by + c = 0.

La distance (d) du point C(x3, y3) à la droite AB (ax + by + c = 0) est donnée par la formule:

d = |ax3 + by3 + c| / √(a² + b²)

Cette distance d correspond à la hauteur du triangle issue du sommet C sur la base AB.

Cas Particuliers

Triangle équilatéral: Tous les côtés sont égaux. La hauteur se calcule par: h = (√3 / 2) * a, où a est la longueur d'un côté.
Triangle isocèle: Deux côtés sont égaux. La hauteur relative à la base (le côté inégal) divise le triangle en deux triangles rectangles égaux. Vous pouvez utiliser le théorème de Pythagore pour trouver la hauteur.
Triangle rectangle: L'un des angles est droit (90 degrés). Les deux côtés adjacents à l'angle droit sont aussi des hauteurs.

En résumé, la méthode la plus appropriée dépend des informations disponibles. Choisir la bonne approche simplifie le calcul. Assurez vous de bien identifier les données connues et la hauteur que vous cherchez à déterminer. L'utilisation correcte des formules et des principes trigonométriques permet de résoudre ces problèmes efficacement.