Comment Démontrer Que Deux Droites Sont Perpendiculaires

Dans le vaste domaine de la géométrie, l'identification de relations angulaires spécifiques entre les lignes est une tâche essentielle. Démontrer la perpendicularité entre deux droites est une compétence fondamentale. Voici plusieurs méthodes pour y parvenir avec rigueur.

On peut utiliser l'angle droit pour démontrer que deux droites sont perpendiculaires. Si l'angle formé par l'intersection de deux droites mesure précisément 90 degrés, elles sont, par définition, perpendiculaires. La mesure de cet angle peut être obtenue à l'aide d'un rapporteur ou par construction géométrique.

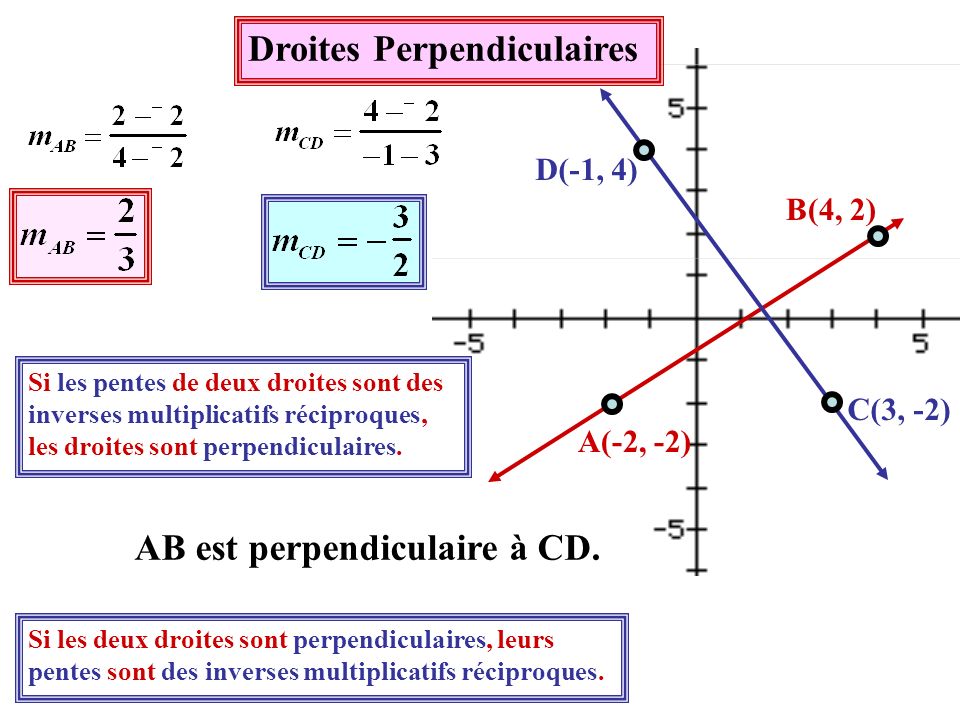
Une approche courante implique l'examen des pentes des droites. Si l'on connaît les équations des droites sous la forme y = mx + b, où m représente la pente, la condition de perpendicularité est facilement vérifiable. Deux droites sont perpendiculaires si et seulement si le produit de leurs pentes est égal à -1. Autrement dit, si la pente d'une droite est m, la pente de la droite perpendiculaire sera -1/m.

Un exemple concret illustre cette méthode. Supposons que nous ayons deux droites : y = 2x + 3 et y = -1/2x - 1. La pente de la première droite est 2 et la pente de la seconde est -1/2. Le produit de ces pentes est 2 * (-1/2) = -1. On peut donc conclure que ces deux droites sont perpendiculaires.

Le Théorème de Pythagore

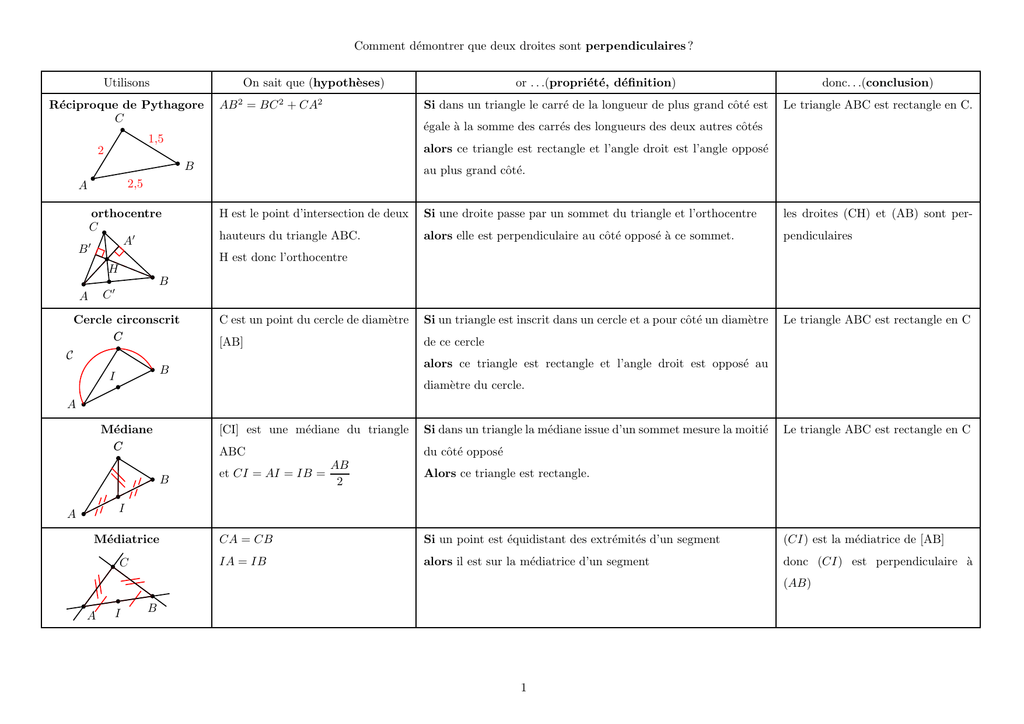
Le théorème de Pythagore offre une autre avenue pour établir la perpendicularité, en particulier lorsque nous connaissons les longueurs des segments de droite formés par l'intersection des droites. Si trois points, A, B et C, forment un triangle et que la relation AB² + BC² = AC² est vérifiée, alors l'angle formé au point B est un angle droit. Par conséquent, les droites AB et BC sont perpendiculaires.

Cette méthode est particulièrement utile lorsque les coordonnées des points sont connues. Calculer les longueurs des segments en utilisant la formule de la distance entre deux points, puis vérifier si le théorème de Pythagore est satisfait permet de conclure à la perpendicularité.

Utilisation des Vecteurs

Dans un contexte plus avancé, l'utilisation des vecteurs permet de démontrer la perpendicularité. Si nous représentons les directions des droites par des vecteurs, deux droites sont perpendiculaires si et seulement si le produit scalaire de leurs vecteurs directeurs est nul.

Soient les vecteurs u et v représentant les directions de deux droites. Si u ⋅ v = 0, alors les droites sont perpendiculaires. Le produit scalaire peut être calculé en utilisant les composantes des vecteurs. Si u = (u₁, u₂) et v = (v₁, v₂), alors u ⋅ v = u₁v₁ + u₂v₂.

Cette méthode est puissante car elle peut être généralisée à des espaces de dimensions supérieures. Elle fournit une approche élégante pour déterminer la perpendicularité dans un contexte vectoriel.

Propriétés des Figures Géométriques

Dans certains cas, les propriétés intrinsèques de figures géométriques spécifiques peuvent simplifier la démonstration de la perpendicularité. Par exemple, les diagonales d'un losange se coupent perpendiculairement. De même, la tangente à un cercle en un point est perpendiculaire au rayon menant à ce point.

Identifier ces propriétés permet de conclure à la perpendicularité sans nécessiter de calculs complexes. La reconnaissance de ces configurations géométriques constitue un atout précieux.

Angles Complémentaires et Supplémentaires

Enfin, l'analyse des angles formés par les droites peut révéler la perpendicularité. Si deux angles sont complémentaires (leur somme est de 90 degrés) et qu'ils sont adjacents, alors les droites formant ces angles sont perpendiculaires. De même, si deux angles sont supplémentaires (leur somme est de 180 degrés) et qu'un des angles est droit, alors l'autre angle est également droit, impliquant la perpendicularité des droites.

L'utilisation de ces relations angulaires, combinée à une connaissance approfondie des théorèmes géométriques fondamentaux, permet d'établir avec certitude la perpendicularité de deux droites. La maîtrise de ces techniques est essentielle pour la résolution de problèmes complexes en géométrie et au-delà.