Calculer L'hypoténuse D'un Triangle Rectangle Avec Un Angle

$Calculer L'hypoténuse D'un Triangle Rectangle Avec Un Angle Calculer la Longueur d'une Hypoténuse avec Pythagore$

Dans le domaine fascinant de la géométrie, le triangle rectangle occupe une place de choix. Sa particularité réside dans la présence d'un angle droit, un atout précieux pour le calcul de son hypoténuse lorsqu'un angle aigu est connu. Plongeons au cœur de cette exploration mathématique.

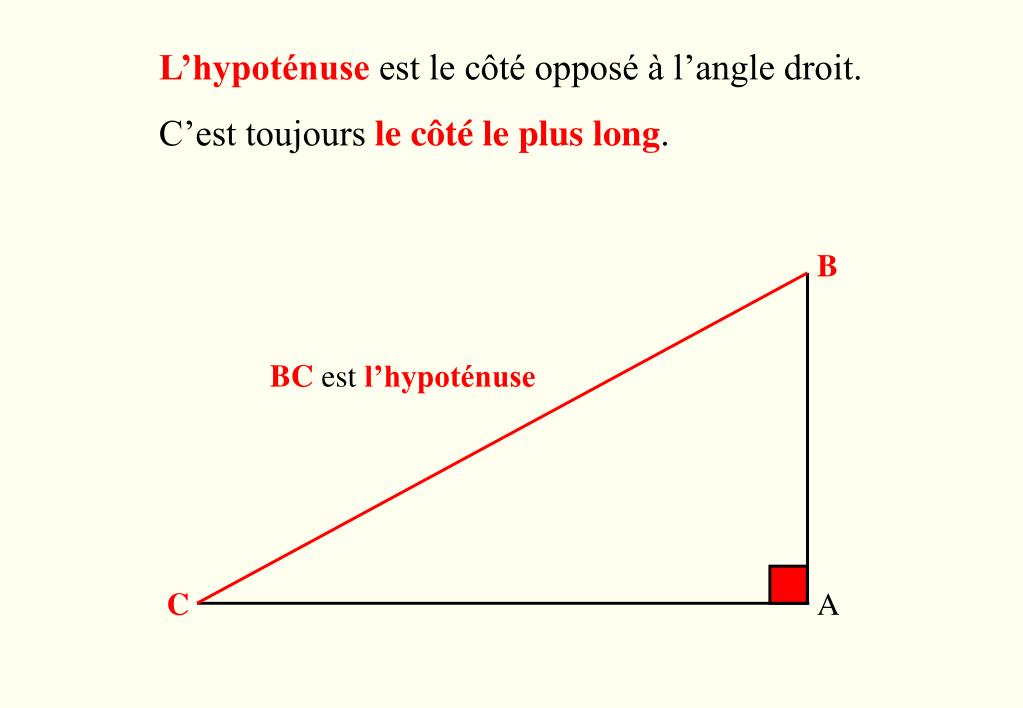
L'hypoténuse, ce côté opposé à l'angle droit, est au centre de notre attention. Sa détermination, loin d'être un mystère impénétrable, repose sur des principes trigonométriques fondamentaux.

Connaissance Préalable Essentielle

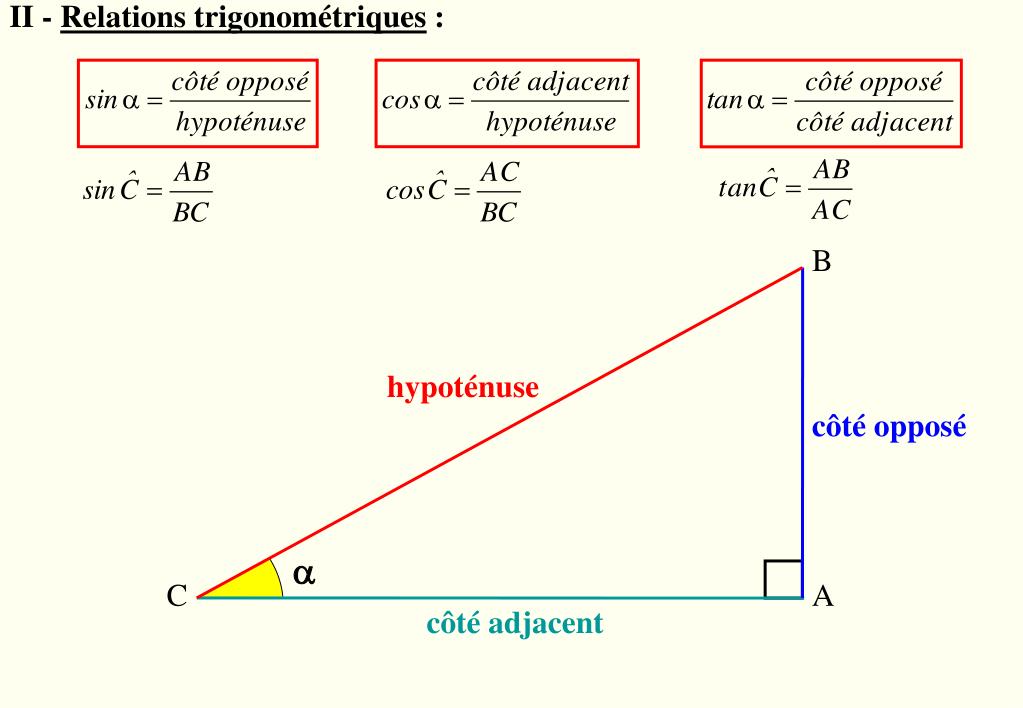
Avant de nous lancer dans les calculs, une brève révision s'impose. Rappelons que les fonctions trigonométriques sinus (sin), cosinus (cos) et tangente (tan) établissent des relations entre les angles et les côtés d'un triangle rectangle.

Le sinus d'un angle (sin θ) est défini comme le rapport entre le côté opposé à cet angle et l'hypoténuse. Le cosinus d'un angle (cos θ) est le rapport entre le côté adjacent à cet angle et l'hypoténuse. La tangente d'un angle (tan θ) est le rapport entre le côté opposé et le côté adjacent.

Méthode Fondée sur le Sinus

Si l'angle aigu connu (θ) est opposé à un côté dont la longueur (a) est également connue, la formule à employer est la suivante :

hypoténuse = a / sin(θ)

Cette formule découle directement de la définition du sinus. Il suffit de diviser la longueur du côté opposé par le sinus de l'angle pour obtenir la longueur de l'hypoténuse.

Méthode Basée sur le Cosinus

Dans le cas où l'angle aigu connu (θ) est adjacent à un côté dont la longueur (b) est connue, l'approche diffère légèrement. La formule à privilégier est alors :

hypoténuse = b / cos(θ)

Ici, nous exploitons la relation entre le cosinus, le côté adjacent et l'hypoténuse. La division de la longueur du côté adjacent par le cosinus de l'angle nous fournit la longueur de l'hypoténuse.

Précautions Cruciales

L'utilisation d'une calculatrice scientifique est indispensable pour déterminer les valeurs du sinus et du cosinus. Assurez-vous que votre calculatrice est réglée sur le mode degré (DEG) si l'angle est exprimé en degrés, ou sur le mode radian (RAD) si l'angle est exprimé en radians. Une erreur de mode peut fausser considérablement les résultats.

Exemple Concret

Considérons un triangle rectangle où l'angle aigu mesure 30 degrés, et le côté opposé à cet angle mesure 5 cm. Nous cherchons à déterminer la longueur de l'hypoténuse.

Nous appliquons la formule : hypoténuse = a / sin(θ)

hypoténuse = 5 cm / sin(30°)

Sachant que sin(30°) = 0,5, nous obtenons :

hypoténuse = 5 cm / 0,5 = 10 cm

L'hypoténuse de ce triangle rectangle mesure donc 10 cm.

Cas Particuliers et Astuces Supplémentaires

Dans certains cas, des angles remarquables tels que 30°, 45° ou 60° sont impliqués. Leurs valeurs trigonométriques sont souvent connues par cœur, ce qui simplifie les calculs. Par exemple, sin(45°) = cos(45°) = √2 / 2.

Si deux angles du triangle rectangle sont connus, le troisième angle peut être facilement déduit, car la somme des angles d'un triangle est toujours égale à 180°. L'angle droit mesurant 90°, la somme des deux angles aigus est donc de 90°.

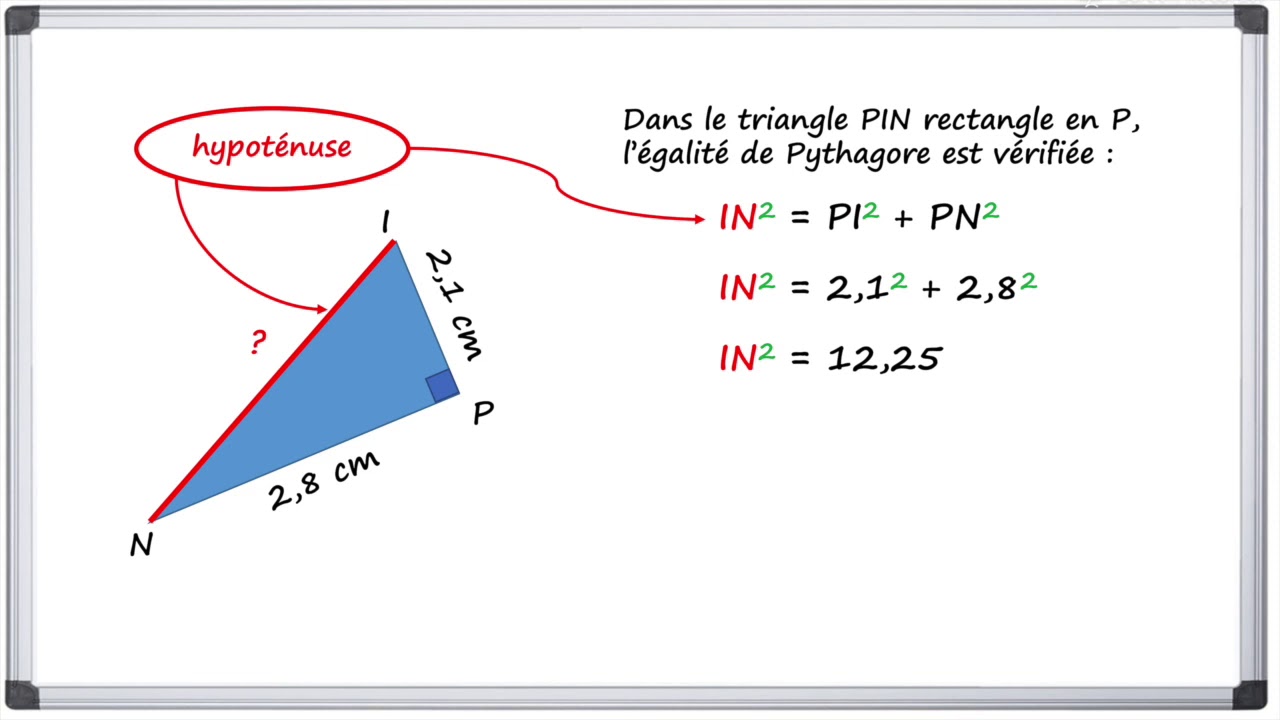
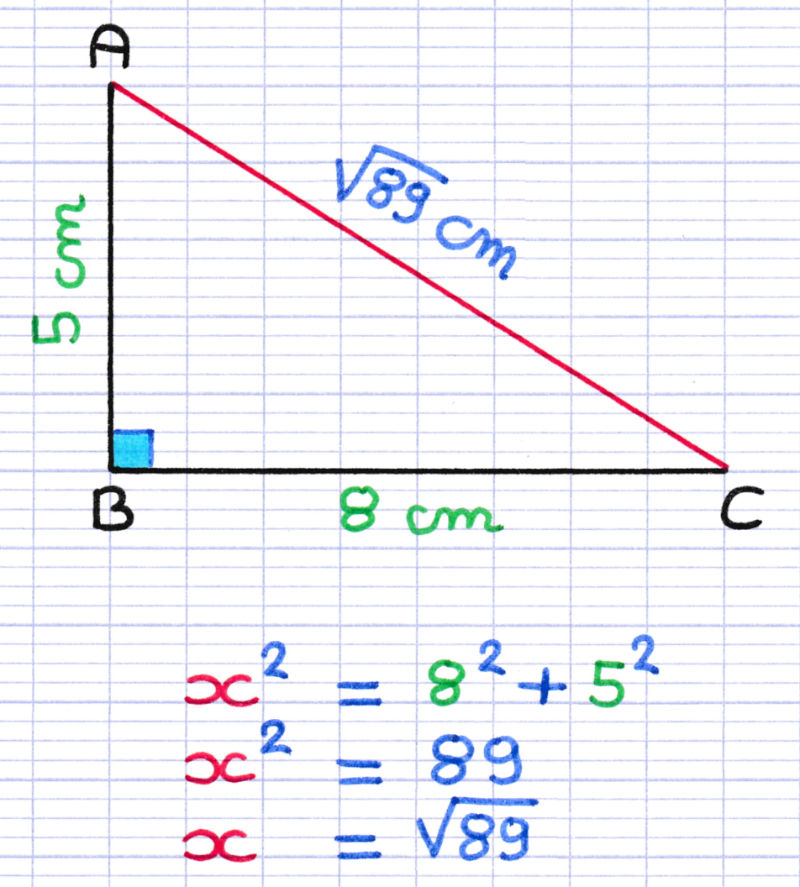
Quand Utiliser le Théorème de Pythagore?

Si les longueurs des deux côtés adjacents à l'angle droit sont connues, il est préférable d'utiliser le théorème de Pythagore (a² + b² = c²) pour calculer l'hypoténuse. Ce théorème établit une relation directe entre les longueurs des côtés d'un triangle rectangle, sans nécessiter l'utilisation de fonctions trigonométriques. Son application est plus directe lorsque l'information sur les angles est absente.

Conclusion

La détermination de l'hypoténuse d'un triangle rectangle à partir d'un angle aigu et de la longueur d'un côté est une procédure rigoureuse, mais accessible grâce à la trigonométrie. La sélection de la formule appropriée (sinus ou cosinus) est cruciale et dépend de la position du côté connu par rapport à l'angle connu. Une rigueur méticuleuse dans l'application des formules et l'utilisation de la calculatrice garantissent l'exactitude des résultats. La maîtrise de ces techniques ouvre les portes à une compréhension plus profonde de la géométrie et de ses applications pratiques.