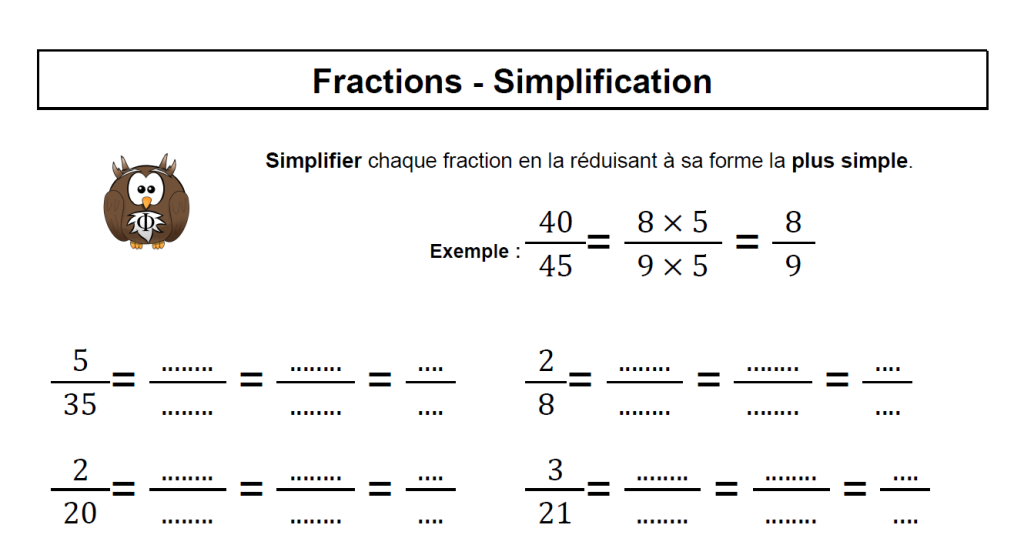
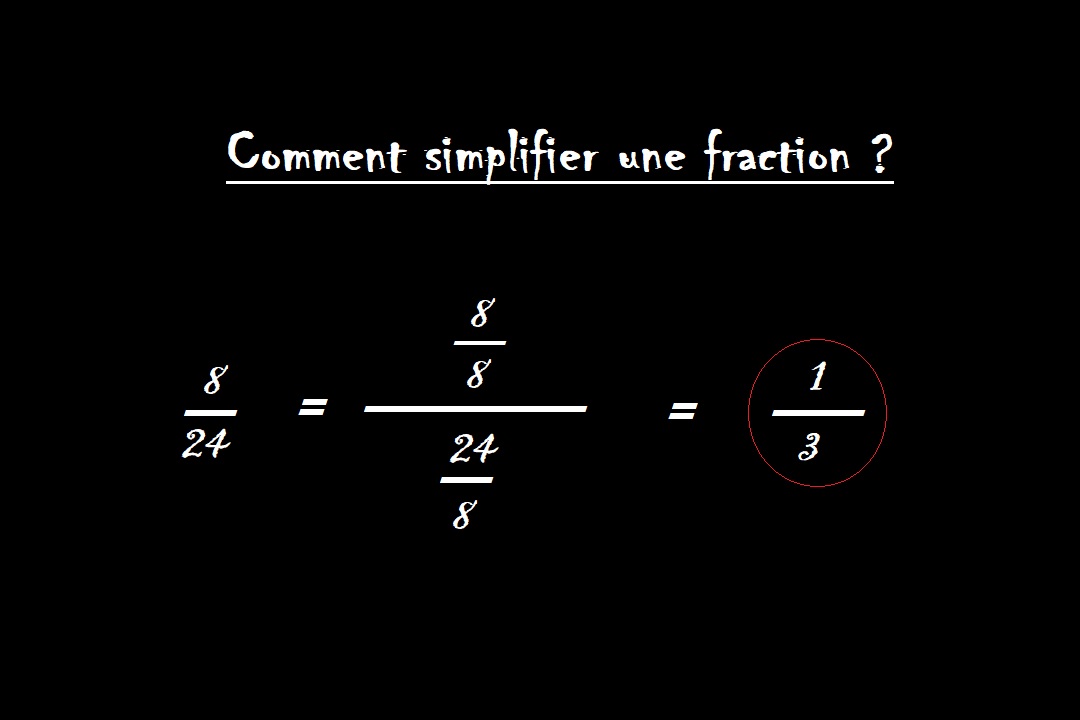Exercice Simplification De Fraction 4ème Avec Correction

$Exercice Simplification De Fraction 4ème Avec Correction Simplifications de fractions - Corrigés d'exercices - AlloSchool$

Dans le domaine des mathématiques de quatrième, la simplification de fractions représente une compétence fondamentale. Elle permet de manipuler les nombres rationnels avec aisance et précision. Notre approche, détaillée et rigoureuse, vise à maîtriser cet art.

Nous débutons par l'identification des facteurs communs. L'objectif est de repérer les diviseurs présents à la fois au numérateur et au dénominateur. Cette étape cruciale nécessite une connaissance approfondie des tables de multiplication et des critères de divisibilité.

Ensuite, nous appliquons la division. On divise le numérateur et le dénominateur par le facteur commun identifié. Cette opération maintient la valeur de la fraction tout en réduisant sa complexité apparente.

La répétition de ce processus est essentielle. On recherche constamment de nouveaux facteurs communs. La simplification continue jusqu'à obtenir une fraction irréductible. Cette fraction ne possède plus de diviseurs communs autres que 1.

Prenons l'exemple de la fraction 24/36. Nous observons que 2 est un facteur commun. Nous divisons donc 24 par 2, obtenant 12. Nous divisons également 36 par 2, obtenant 18. La fraction devient alors 12/18.

Nous remarquons que 12/18 peut encore être simplifiée. 6 est un facteur commun. Nous divisons 12 par 6, obtenant 2. Nous divisons 18 par 6, obtenant 3. La fraction se simplifie à 2/3.

La fraction 2/3 est irréductible. Il n'existe aucun facteur commun entre 2 et 3 autre que 1. Ainsi, la simplification de 24/36 est achevée.

Un autre exemple illustratif est la fraction 45/75. Nous identifions 5 comme facteur commun. Nous divisons 45 par 5, ce qui donne 9. Nous divisons 75 par 5, ce qui donne 15. La fraction se transforme en 9/15.

Nous poursuivons la simplification de 9/15. 3 est un facteur commun évident. Nous divisons 9 par 3, obtenant 3. Nous divisons 15 par 3, obtenant 5. La fraction devient 3/5.

La fraction 3/5 est une fraction irréductible. Il n'y a plus de facteurs communs entre 3 et 5. La simplification de 45/75 aboutit donc à 3/5.

Pour les fractions plus complexes, la décomposition en facteurs premiers est une méthode puissante. Elle consiste à exprimer le numérateur et le dénominateur comme un produit de nombres premiers.

Par exemple, considérons la fraction 168/210. Nous décomposons 168 en 2 x 2 x 2 x 3 x 7. Nous décomposons également 210 en 2 x 3 x 5 x 7.

Ensuite, nous identifions les facteurs communs. Nous observons que 2, 3 et 7 sont présents à la fois dans la décomposition de 168 et de 210.

Nous simplifions en annulant les facteurs communs. Nous annulons un facteur 2, un facteur 3 et un facteur 7. Il reste alors 2 x 2 au numérateur et 5 au dénominateur.

La fraction simplifiée est donc 4/5. Cette méthode, bien que plus élaborée, garantit une simplification précise même pour les fractions les plus complexes.

Il est important de maîtriser les critères de divisibilité. La divisibilité par 2, 3, 5, 9 et 10 est particulièrement utile. La divisibilité par 2 concerne les nombres pairs. La divisibilité par 3 s'applique lorsque la somme des chiffres est divisible par 3. La divisibilité par 5 concerne les nombres se terminant par 0 ou 5. La divisibilité par 9 est similaire à celle de 3. La divisibilité par 10 concerne les nombres se terminant par 0.

Ces critères accélèrent l'identification des facteurs communs. Ils permettent de simplifier les fractions plus rapidement.

L'entraînement régulier est crucial. La pratique constante renforce la compréhension et l'automatisation des techniques de simplification. Des exercices variés, allant des plus simples aux plus complexes, sont essentiels.

L'utilisation d'outils de vérification est également recommandée. Les calculatrices et les applications en ligne peuvent confirmer l'exactitude des résultats. Cependant, il est important de comprendre le processus de simplification et de ne pas se fier uniquement à ces outils.

La simplification de fractions est une compétence essentielle. Elle est utilisée dans de nombreux domaines des mathématiques. Une maîtrise solide de cette compétence facilite l'apprentissage des concepts plus avancés. Elle prépare également les élèves aux défis mathématiques futurs.

Une attention particulière doit être portée aux erreurs courantes. L'oubli de simplifier complètement une fraction est une erreur fréquente. L'identification incorrecte des facteurs communs en est une autre. La pratique régulière et la vérification des résultats permettent de minimiser ces erreurs.

En conclusion, la simplification de fractions est une compétence fondamentale. La maîtrise de cette compétence repose sur une connaissance approfondie des facteurs communs, des critères de divisibilité et des techniques de décomposition. Une pratique régulière et une attention particulière aux erreurs courantes sont essentielles pour atteindre une maîtrise complète.