Démontrer Que Deux Droites Sont Parallèles Avec Les Coordonnées

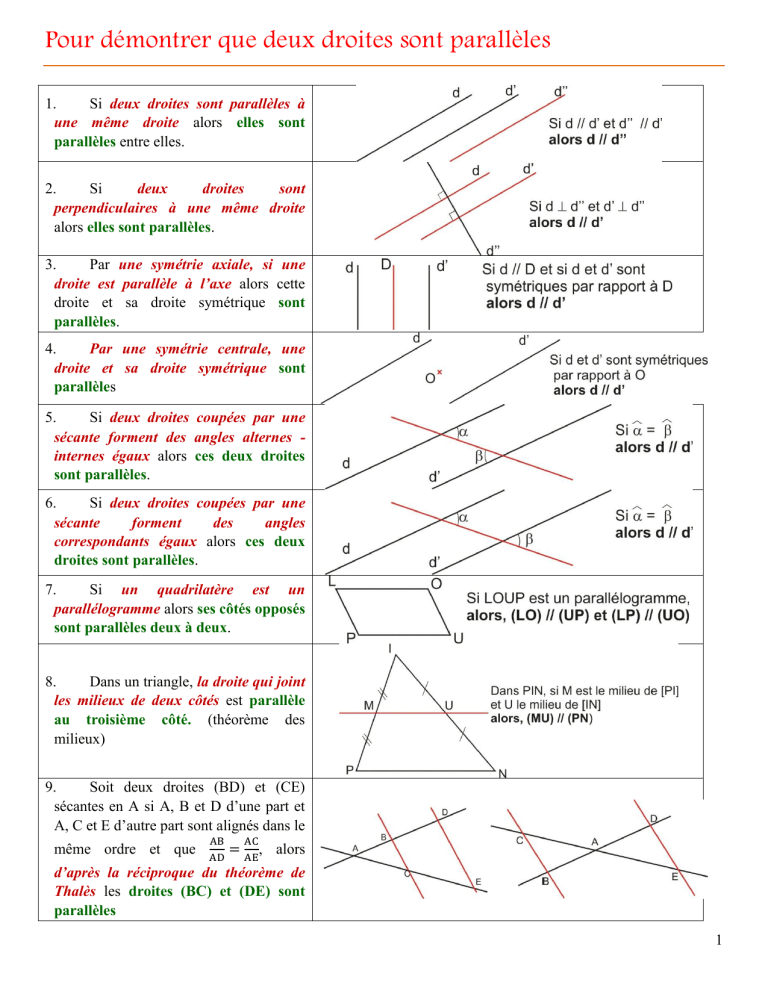
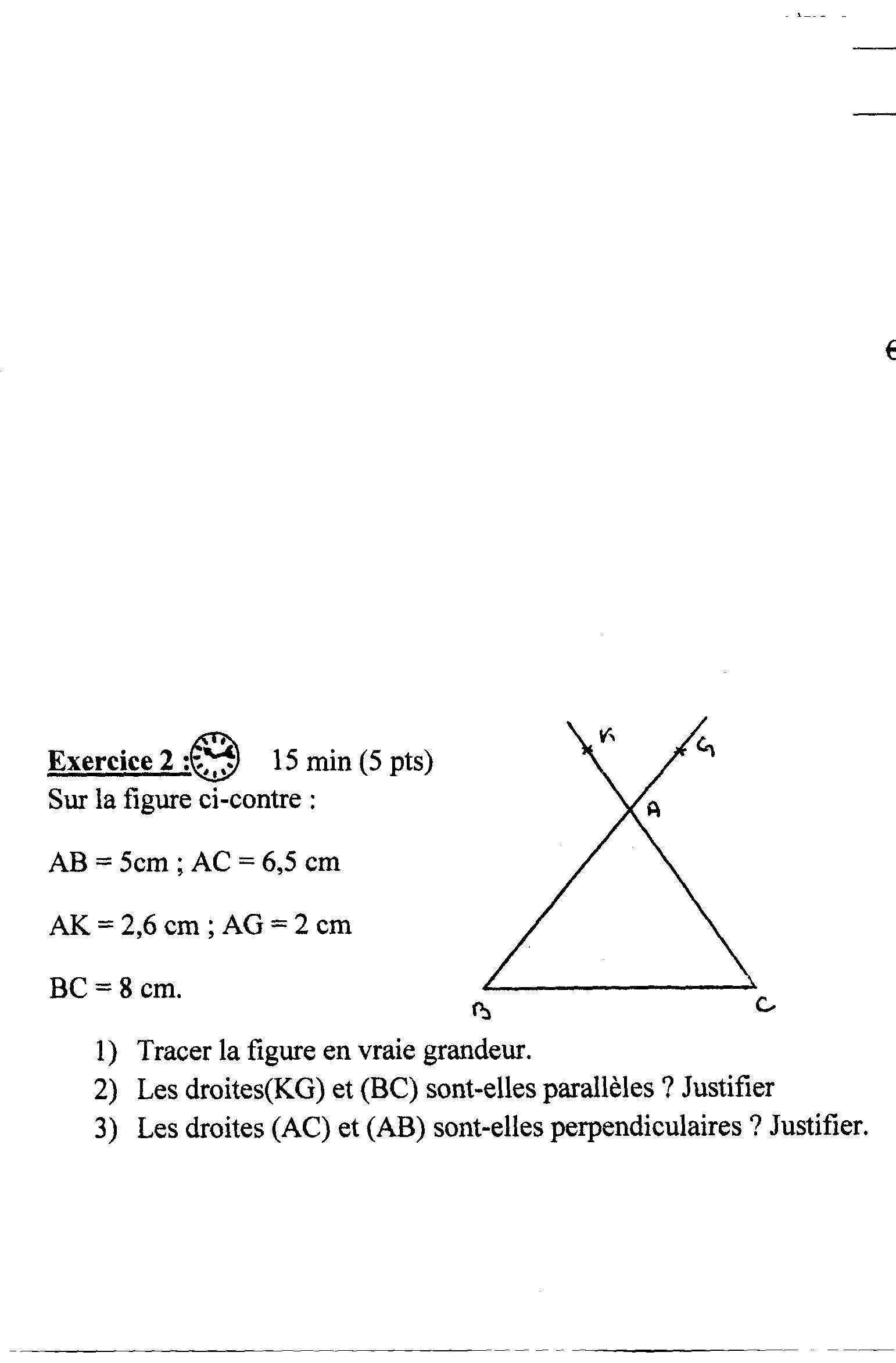
Dans le vaste domaine de la géométrie analytique, établir le parallélisme entre deux droites à l'aide de leurs coordonnées est une compétence fondamentale. Nous allons explorer les méthodes rigoureuses pour accomplir cette tâche avec précision et assurance.

Déterminer le Coefficient Directeur

La pierre angulaire de notre approche réside dans le coefficient directeur, souvent noté 'm'. Il caractérise l'inclinaison d'une droite par rapport à l'axe des abscisses. Pour une droite définie par deux points distincts, disons A(x₁, y₁) et B(x₂, y₂), le coefficient directeur se calcule comme suit:

m = (y₂ - y₁) / (x₂ - x₁)

Cette formule simple, mais puissante, nous donne une mesure quantifiable de la pente de la droite. Assurez-vous que x₁ ≠ x₂, sinon nous serions confrontés à une division par zéro, indiquant une droite verticale.

Si l'équation de la droite est donnée sous la forme y = mx + b, alors le coefficient directeur est directement identifié comme le coefficient 'm' devant la variable 'x'. Cette forme, dite réduite, offre une lecture immédiate de l'inclinaison.

Le Critère Fondamental du Parallélisme

Deux droites sont parallèles si et seulement si leurs coefficients directeurs sont égaux. C'est un principe absolu. Si nous avons deux droites, disons D₁ et D₂, avec des coefficients directeurs respectifs m₁ et m₂, alors D₁ est parallèle à D₂ si et seulement si m₁ = m₂.

La démonstration de ce critère est rigoureuse. Si m₁ = m₂, alors les droites ont la même inclinaison et, par conséquent, ne se croiseront jamais. Si m₁ ≠ m₂, alors les droites ont des inclinaisons différentes et se croiseront inévitablement en un point.

Application Pratique: Démonstration avec les Coordonnées

Considérons deux droites, D₁ définie par les points A(1, 3) et B(4, 9), et D₂ définie par les points C(2, 1) et D(5, 7).

Calculons le coefficient directeur de D₁:

m₁ = (9 - 3) / (4 - 1) = 6 / 3 = 2

Calculons le coefficient directeur de D₂:

m₂ = (7 - 1) / (5 - 2) = 6 / 3 = 2

Comme m₁ = m₂ = 2, nous pouvons conclure que les droites D₁ et D₂ sont parallèles. Aucun doute n'est permis.

Cas Particuliers et Précautions

Les droites verticales méritent une attention particulière. Une droite verticale a une équation de la forme x = c, où c est une constante. Le coefficient directeur est indéfini, car le dénominateur de la formule serait zéro. Deux droites verticales sont toujours parallèles entre elles. Une droite verticale n'est jamais parallèle à une droite horizontale (y = k, où k est une constante).

Il est crucial d'être précis dans les calculs. Une erreur mineure dans les coordonnées ou dans l'application de la formule du coefficient directeur peut conduire à une conclusion erronée. Vérifiez toujours vos calculs.

Démonstration Analytique Approfondie

Supposons que nous ayons deux droites, D₁ et D₂, définies par les équations suivantes:

D₁: a₁x + b₁y + c₁ = 0 D₂: a₂x + b₂y + c₂ = 0

Nous pouvons réécrire ces équations sous la forme réduite (y = mx + b), à condition que b₁ et b₂ soient non nuls:

D₁: y = (-a₁/b₁)x - (c₁/b₁) D₂: y = (-a₂/b₂)x - (c₂/b₂)

Par conséquent, les coefficients directeurs sont:

m₁ = -a₁/b₁ m₂ = -a₂/b₂

Pour que D₁ et D₂ soient parallèles, il faut que m₁ = m₂, donc:

-a₁/b₁ = -a₂/b₂

Ce qui implique:

a₁/b₁ = a₂/b₂

Ou encore:

a₁b₂ = a₂b₁

Cette relation, a₁b₂ = a₂b₁, est une condition nécessaire et suffisante pour que les droites D₁ et D₂ soient parallèles, lorsqu'elles sont exprimées sous leur forme générale. Si b₁ ou b₂ est nul, cela signifie que la droite correspondante est verticale, et nous devons revenir à la considération des droites verticales.

Exemple d'Application Avancée

Soit deux droites définies par les équations :

D₁: 2x + 3y - 5 = 0 D₂: 4x + 6y + 1 = 0

Vérifions si la condition a₁b₂ = a₂b₁ est satisfaite :

a₁ = 2, b₁ = 3 a₂ = 4, b₂ = 6

Calculons :

a₁b₂ = 2 * 6 = 12 a₂b₁ = 4 * 3 = 12

Comme a₁b₂ = a₂b₁, les droites D₁ et D₂ sont parallèles.

Conclusion

Démontrer que deux droites sont parallèles à partir de leurs coordonnées repose sur la compréhension et l'application rigoureuse du concept de coefficient directeur. Que ce soit par le calcul direct à partir de deux points, par l'identification dans l'équation réduite de la droite, ou par l'utilisation de la condition a₁b₂ = a₂b₁ pour les équations générales, la maîtrise de ces techniques garantit une conclusion précise et justifiée. La géométrie analytique, lorsqu'elle est abordée avec soin et rigueur, révèle sa puissance et son élégance.