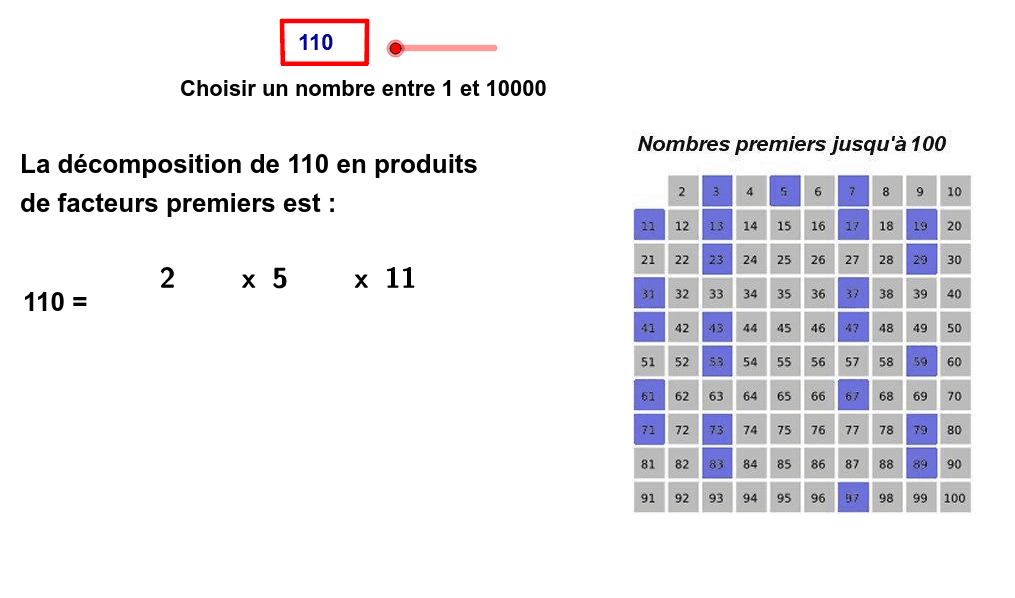
Décomposer Chaque Nombre En Produit De Facteurs Premiers

Décomposer un nombre en produit de facteurs premiers est fondamental. Cela révèle sa structure multiplicative. Chaque nombre entier supérieur à 1 peut être exprimé ainsi. La décomposition est unique, abstraction faite de l'ordre des facteurs.

Pour décomposer, on commence par diviser le nombre par le plus petit nombre premier possible, 2. Si la division est entière, on note 2 comme facteur. On continue avec le quotient obtenu. On répète le processus avec 2 tant que c'est possible.

Si 2 ne divise plus, on passe au nombre premier suivant, 3. On divise par 3 autant de fois que possible. On note 3 comme facteur à chaque division entière. On continue ainsi avec les nombres premiers suivants : 5, 7, 11, 13, etc.

On s'arrête lorsque le quotient obtenu est lui-même un nombre premier. Ce dernier nombre premier est aussi un facteur. La liste de tous les facteurs premiers trouvés, multipliés entre eux, donne le nombre initial.

Prenons l'exemple de 24. 24 est divisible par 2. 24 / 2 = 12. On note 2. 12 est divisible par 2. 12 / 2 = 6. On note 2. 6 est divisible par 2. 6 / 2 = 3. On note 2. 3 est un nombre premier. On note 3. La décomposition de 24 est donc 2 x 2 x 2 x 3, soit 2³ x 3.

Prenons l'exemple de 75. 75 n'est pas divisible par 2. 75 est divisible par 3. 75 / 3 = 25. On note 3. 25 n'est pas divisible par 3. 25 est divisible par 5. 25 / 5 = 5. On note 5. 5 est un nombre premier. On note 5. La décomposition de 75 est donc 3 x 5 x 5, soit 3 x 5².

L'utilisation d'un arbre de facteurs peut faciliter la visualisation. On part du nombre à décomposer. On le divise en deux branches, représentant deux facteurs. Si l'un des facteurs n'est pas premier, on le divise à nouveau en deux branches. On continue jusqu'à n'avoir que des nombres premiers aux extrémités des branches.

La décomposition en facteurs premiers est utile pour plusieurs opérations. Elle simplifie le calcul du Plus Grand Commun Diviseur (PGCD). Elle simplifie le calcul du Plus Petit Commun Multiple (PPCM). Elle permet de simplifier des fractions. Elle révèle les propriétés d'un nombre.

Techniques Avancées

Pour les grands nombres, la méthode de division successive peut être longue. Des algorithmes plus efficaces existent. Le test de primalité de Miller-Rabin permet de déterminer rapidement si un nombre est premier. L'algorithme rho de Pollard est utilisé pour trouver un facteur non trivial d'un nombre composé. La crible quadratique est une autre méthode de factorisation.

La factorisation de grands nombres est un problème complexe. La difficulté de factoriser certains nombres est à la base de la cryptographie moderne. L'algorithme RSA utilise cette difficulté pour sécuriser les communications.

La décomposition en facteurs premiers n'est pas toujours unique dans les anneaux autres que les entiers. Cependant, dans l'ensemble des entiers, elle l'est. C'est un théorème fondamental de l'arithmétique.

Exemples Supplémentaires

Décomposons 120. 120 = 2 x 60. 60 = 2 x 30. 30 = 2 x 15. 15 = 3 x 5. Donc, 120 = 2 x 2 x 2 x 3 x 5 = 2³ x 3 x 5.

Décomposons 360. 360 = 2 x 180. 180 = 2 x 90. 90 = 2 x 45. 45 = 3 x 15. 15 = 3 x 5. Donc, 360 = 2 x 2 x 2 x 3 x 3 x 5 = 2³ x 3² x 5.

Décomposons 1001. 1001 = 7 x 143. 143 = 11 x 13. Donc, 1001 = 7 x 11 x 13.

Décomposons 2025. 2025 = 3 x 675. 675 = 3 x 225. 225 = 3 x 75. 75 = 3 x 25. 25 = 5 x 5. Donc, 2025 = 3 x 3 x 3 x 3 x 5 x 5 = 3⁴ x 5².

La maîtrise de la décomposition en facteurs premiers est essentielle. Elle facilite la manipulation des nombres. Elle permet de mieux comprendre leurs propriétés. C'est un outil puissant en mathématiques.

L'utilisation de logiciels de calcul formel (CAS) comme Mathematica ou SageMath permet d'automatiser la décomposition en facteurs premiers. Ces outils peuvent traiter des nombres beaucoup plus grands que ceux que l'on peut factoriser à la main. Ils utilisent des algorithmes sophistiqués pour optimiser le processus.

La décomposition en facteurs premiers est un concept fondamental de la théorie des nombres. Elle est utilisée dans de nombreux domaines de la mathématique et de l'informatique. Sa compréhension approfondie est donc cruciale.