Comment Trouver Une Longueur Dans Un Triangle Rectangle

Dans le domaine fascinant de la géométrie, le triangle rectangle se distingue par ses propriétés uniques et sa présence omniprésente dans de nombreux problèmes mathématiques et applications pratiques. Déterminer la longueur d'un côté inconnu dans un triangle rectangle est une compétence fondamentale. Cet article vous offre une exploration exhaustive des méthodes à votre disposition.

Le Théorème de Pythagore : L'outil fondamental

Le théorème de Pythagore constitue la pierre angulaire du calcul des longueurs dans un triangle rectangle. Il stipule que le carré de la longueur de l'hypoténuse (le côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des deux autres côtés, appelés cathètes.

Mathématiquement, cela s'exprime ainsi :

a² + b² = c²

Où :

a et b sont les longueurs des cathètes.
c est la longueur de l'hypoténuse.

Application du Théorème:

Pour utiliser le théorème de Pythagore, vous devez connaître la longueur d'au moins deux côtés du triangle rectangle.

Si vous connaissez les longueurs des deux cathètes (a et b) : Vous pouvez calculer la longueur de l'hypoténuse (c) en effectuant la racine carrée de la somme des carrés de a et b : c = √(a² + b²).
Si vous connaissez la longueur de l'hypoténuse (c) et la longueur d'une cathète (par exemple, a) : Vous pouvez calculer la longueur de l'autre cathète (b) en effectuant la racine carrée de la différence entre le carré de c et le carré de a : b = √(c² - a²).

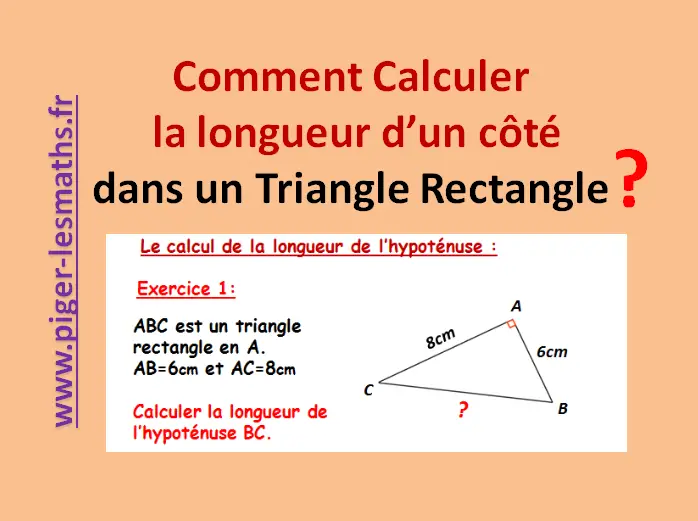
Exemple:

Considérons un triangle rectangle où une cathète mesure 3 cm et l'autre 4 cm. Pour trouver la longueur de l'hypoténuse, nous appliquons le théorème :

c² = 3² + 4² = 9 + 16 = 25

c = √25 = 5 cm

L'hypoténuse mesure donc 5 cm.

Utilisation des Rapports Trigonométriques

Lorsque l'information disponible inclut un angle aigu (autre que l'angle droit) et la longueur d'un côté, les rapports trigonométriques s'avèrent indispensables. Les trois principaux rapports trigonométriques sont :

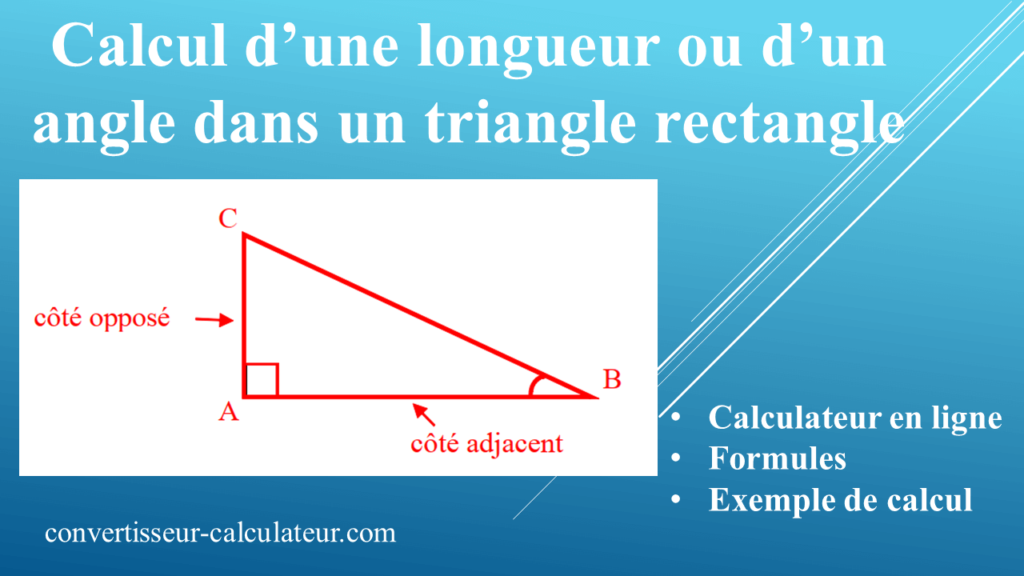
Sinus (sin) : Le sinus d'un angle est égal au rapport entre la longueur du côté opposé à cet angle et la longueur de l'hypoténuse. sin(θ) = côté opposé / hypoténuse
Cosinus (cos) : Le cosinus d'un angle est égal au rapport entre la longueur du côté adjacent à cet angle et la longueur de l'hypoténuse. cos(θ) = côté adjacent / hypoténuse
Tangente (tan) : La tangente d'un angle est égale au rapport entre la longueur du côté opposé à cet angle et la longueur du côté adjacent à cet angle. tan(θ) = côté opposé / côté adjacent

Application des Rapports Trigonométriques:

Identifiez l'angle aigu connu (θ).
Identifiez le côté connu et le côté dont vous cherchez la longueur.
Choisissez le rapport trigonométrique approprié en fonction des côtés impliqués.
- Si vous connaissez le côté opposé et l'hypoténuse, utilisez le sinus.
- Si vous connaissez le côté adjacent et l'hypoténuse, utilisez le cosinus.
- Si vous connaissez le côté opposé et le côté adjacent, utilisez la tangente.
Écrivez l'équation trigonométrique et résolvez-la pour trouver la longueur inconnue.

Exemple:

Supposons que dans un triangle rectangle, un angle aigu mesure 30° et le côté opposé à cet angle mesure 6 cm. Pour trouver la longueur de l'hypoténuse, nous utilisons le sinus :

sin(30°) = 6 cm / hypoténuse

hypoténuse = 6 cm / sin(30°)

Puisque sin(30°) = 0.5,

hypoténuse = 6 cm / 0.5 = 12 cm

L'hypoténuse mesure donc 12 cm.

Triangles Rectangles Spéciaux

Certains triangles rectangles présentent des propriétés spécifiques qui simplifient le calcul des longueurs. Les deux types les plus courants sont :

Le triangle 30-60-90 : Dans ce triangle, les angles mesurent 30°, 60° et 90°. Les longueurs des côtés suivent une relation précise : si le côté opposé à l'angle de 30° mesure x, alors le côté opposé à l'angle de 60° mesure x√3, et l'hypoténuse mesure 2x.
Le triangle 45-45-90 : Dans ce triangle, les angles mesurent 45°, 45° et 90°. Les deux cathètes sont de même longueur (disons x), et l'hypoténuse mesure x√2.

Application des Propriétés des Triangles Spéciaux:

Si vous identifiez un triangle rectangle comme étant l'un de ces types spéciaux, vous pouvez déterminer rapidement les longueurs des côtés en utilisant les relations mentionnées ci-dessus, connaissant la longueur d'un seul côté.

Exemple:

Si dans un triangle 30-60-90, le côté opposé à l'angle de 30° mesure 4 cm, alors :

Le côté opposé à l'angle de 60° mesure 4√3 cm.
L'hypoténuse mesure 2 * 4 cm = 8 cm.

Choisir la Méthode Appropriée

Le choix de la méthode dépend de l'information fournie :

Si vous connaissez les longueurs de deux côtés : Utilisez le théorème de Pythagore.
Si vous connaissez la longueur d'un côté et la mesure d'un angle aigu : Utilisez les rapports trigonométriques.
Si vous reconnaissez un triangle rectangle spécial (30-60-90 ou 45-45-90) : Utilisez les relations spécifiques à ce type de triangle.

Maîtriser ces techniques vous permettra de naviguer avec assurance dans les problèmes impliquant des triangles rectangles et de déterminer les longueurs inconnues avec précision. La pratique régulière est essentielle pour consolider ces connaissances et développer une intuition géométrique.