Comment Trouver Le Point D Intersection De Deux Droites

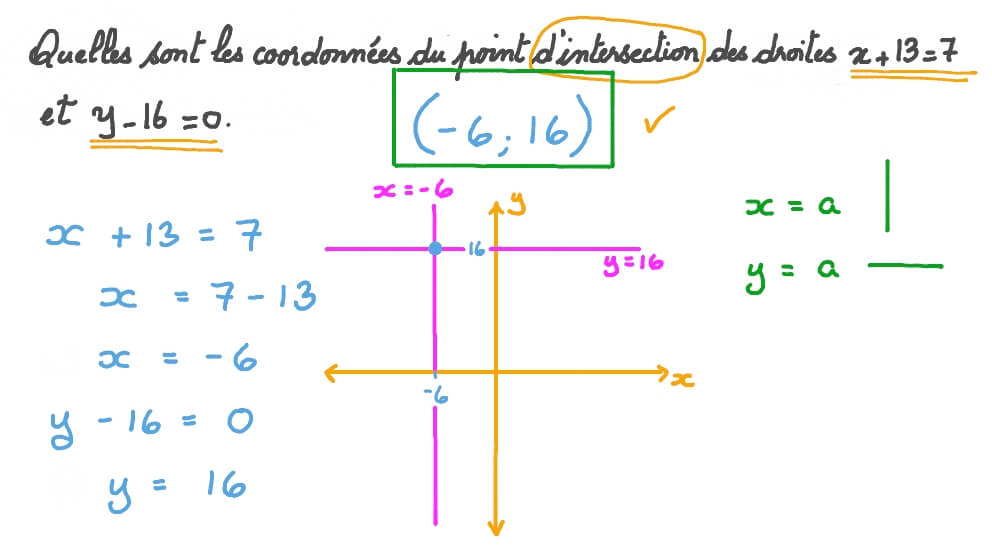
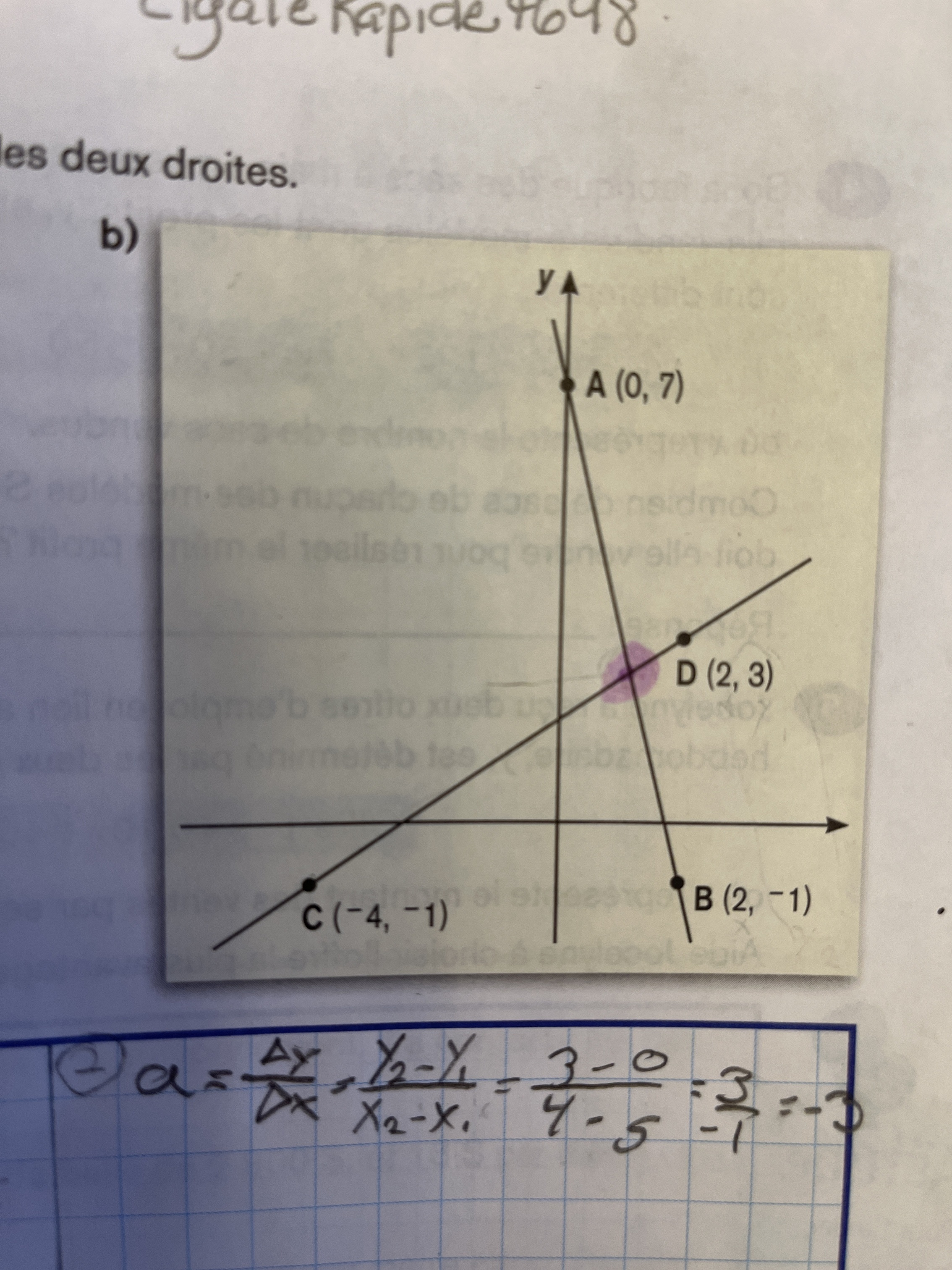
Voici une méthode exhaustive pour déterminer le point d'intersection de deux droites.

Nous allons aborder différentes situations. Chaque situation nécessitera une approche spécifique.

Droites Définies par des Équations Cartésiennes

Considérons deux droites, D1 et D2. Elles sont définies par les équations suivantes :

D1: a1x + b1y + c1 = 0 D2: a2x + b2y + c2 = 0

Pour trouver le point d'intersection, résolvez le système d'équations. Plusieurs méthodes sont possibles.

Méthode de Substitution:

Exprimez y en fonction de x dans l'une des équations. Remplacez cette expression de y dans l'autre équation. Résolvez l'équation résultante pour trouver la valeur de x. Substituez la valeur de x dans l'une des équations originales pour trouver la valeur de y.
Méthode d'Élimination:

Multipliez chaque équation par une constante appropriée. L'objectif est d'avoir les coefficients de x (ou y) égaux en valeur absolue mais de signe opposé. Additionnez les deux équations. Ceci éliminera x (ou y). Résolvez l'équation résultante pour trouver la valeur de la variable restante. Substituez cette valeur dans l'une des équations originales pour trouver la valeur de l'autre variable.

Le couple (x, y) ainsi obtenu représente les coordonnées du point d'intersection.

Droites Définies par des Équations Réduites (Forme y = mx + b)

Si les droites D1 et D2 sont définies par les équations :

D1: y = m1x + b1 D2: y = m2x + b2

où m1 et m2 sont les pentes et b1 et b2 sont les ordonnées à l'origine.

Pour trouver l'intersection, égalisez les deux expressions pour y:

m1x + b1 = m2x + b2

Résolvez cette équation pour x:

x = (b2 - b1) / (m1 - m2)

(Notez que cette méthode ne fonctionne que si m1 ≠ m2. Si m1 = m2, les droites sont parallèles ou confondues.)

Substituez la valeur de x dans l'une des équations y = m1x + b1 ou y = m2x + b2 pour trouver la valeur de y.

Le couple (x, y) représente les coordonnées du point d'intersection.

Droites Définies par des Représentations Paramétriques

Considérons deux droites D1 et D2 définies paramétriquement:

D1: x = x1 + tv1x*; y = y1 + tv1y D2: x = x2 + sv2x*; y = y2 + sv2y

où (x1, y1) et (x2, y2) sont des points sur les droites, et (v1x, v1y) et (v2x, v2y) sont les vecteurs directeurs. t et s sont des paramètres réels.

Pour trouver l'intersection, égalisez les expressions pour x et y:

x1 + tv1x* = x2 + sv2x y1 + tv1y* = y2 + sv2y

Vous obtenez un système de deux équations à deux inconnues (t et s). Résolvez ce système. Vous pouvez utiliser la substitution ou l'élimination.

Si une solution existe pour t et s, substituez la valeur de t dans l'équation paramétrique de D1 (ou la valeur de s dans l'équation de D2) pour trouver les coordonnées (x, y) du point d'intersection.

Si le système n'a pas de solution, les droites sont parallèles et ne se coupent pas. Si le système a une infinité de solutions, les droites sont confondues.

Cas Particuliers et Vérifications

Droites Parallèles: Si, dans la forme y = mx + b, m1 = m2 et b1 ≠ b2, les droites sont parallèles et ne se coupent pas. Si les droites sont définies cartésiennement, le déterminant de la matrice des coefficients a1b2 - a2b1 = 0 mais a1c2-a2c1 ≠ 0.
Droites Perpendiculaires: Les droites sont perpendiculaires si le produit de leurs pentes est -1 (m1 m2 = -1). L'intersection se trouve comme décrit précédemment.
Droites Confondues: Si m1 = m2 et b1 = b2, les droites sont identiques (confondues). Dans ce cas, il n'y a pas un seul point d'intersection, mais une infinité (tous les points sur la droite). Dans la forme cartésienne a1/a2 = b1/b2 = c1/c2.
Vérification: Après avoir trouvé les coordonnées (x, y) du point d'intersection, substituez ces valeurs dans les équations originales des droites. Les équations doivent être satisfaites pour confirmer que le point est bien sur les deux droites.

Exemple Numérique (Equations Réduites)

Soient les droites :

D1: y = 2x + 1 D2: y = -x + 4

Egalisons les expressions pour y:

2x + 1 = -x + 4 3x = 3 x = 1

Substituons x = 1 dans D1:

y = 2(1) + 1 = 3

Le point d'intersection est (1, 3).

Exemple Numérique (Equations Cartésiennes)

Soient les droites :

D1: x + y - 5 = 0 D2: 2x - y - 1 = 0

Utilisons l'élimination. Additionnons les deux équations:

3x - 6 = 0 x = 2

Substituons x = 2 dans D1:

2 + y - 5 = 0 y = 3

Le point d'intersection est (2, 3).

L'application rigoureuse de ces méthodes garantit la détermination précise du point d'intersection de deux droites, quel que soit leur mode de définition.