Comment Representer Une Fonction Affine Graphiquement

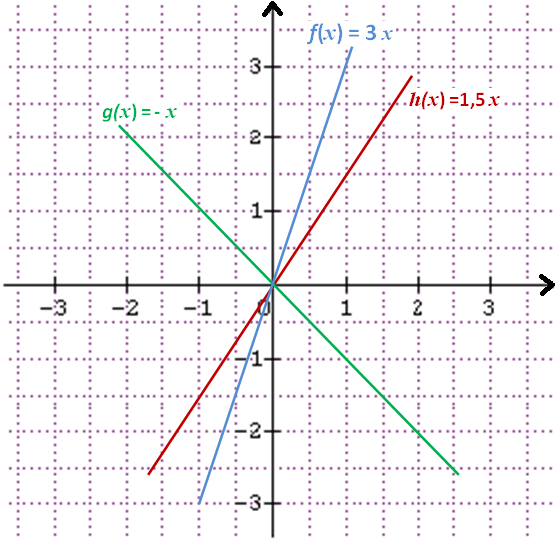
Une fonction affine se représente graphiquement par une droite. La maîtrise de cette représentation est cruciale.

Tracer une fonction affine à partir de son équation

L'équation générale d'une fonction affine est f(x) = ax + b. 'a' est le coefficient directeur. 'b' est l'ordonnée à l'origine.

Identifiez 'a' et 'b' dans l'équation donnée.
Placez le point d'ordonnée 'b' sur l'axe des ordonnées (l'axe vertical). C'est le point (0, b).
Utilisez le coefficient directeur 'a' pour trouver un deuxième point. 'a' représente la pente de la droite. Si 'a' est positif, la droite monte de gauche à droite. Si 'a' est négatif, la droite descend de gauche à droite.
Interprétez 'a' comme une fraction. Si 'a' = 2, considérez que 'a' = 2/1. Si 'a' = -3/4, la fraction est déjà définie.
À partir du point (0, b), déplacez-vous horizontalement de la valeur du dénominateur (vers la droite).
Déplacez-vous verticalement de la valeur du numérateur. Montez si le numérateur est positif. Descendez si le numérateur est négatif.
Vous obtenez ainsi un deuxième point.
Tracez une droite passant par les deux points identifiés. Cette droite représente graphiquement la fonction affine.
Vérifiez que la droite prolonge correctement la tendance définie par 'a'.

Exemple concret : f(x) = 2x + 1

a = 2 et b = 1.
Placez le point (0, 1) sur l'axe des ordonnées.
a = 2/1.
À partir de (0, 1), déplacez-vous de 1 unité vers la droite.
Déplacez-vous de 2 unités vers le haut.
Vous obtenez le point (1, 3).
Tracez la droite passant par (0, 1) et (1, 3).

Exemple concret : f(x) = -x + 3

a = -1 et b = 3.
Placez le point (0, 3) sur l'axe des ordonnées.
a = -1/1.
À partir de (0, 3), déplacez-vous de 1 unité vers la droite.
Déplacez-vous de 1 unité vers le bas.
Vous obtenez le point (1, 2).
Tracez la droite passant par (0, 3) et (1, 2).

Tracer une fonction affine à partir de deux points

Si deux points de la droite sont connus, placez ces deux points sur le graphique.
Tracez une droite passant par ces deux points. Cette droite représente la fonction affine.
Assurez-vous que la droite s'étend au-delà des deux points.

Lecture graphique d'une fonction affine

Identifiez l'ordonnée à l'origine. C'est le point où la droite coupe l'axe des ordonnées.
Choisissez deux points distincts sur la droite.
Calculez la variation en y (Δy) entre ces deux points.
Calculez la variation en x (Δx) entre ces deux points.
Le coefficient directeur 'a' est égal à Δy / Δx.
L'équation de la fonction affine est f(x) = ax + b. Remplacez 'a' et 'b' par les valeurs trouvées.

Cas particuliers

Si a = 0, la fonction est constante. La droite est horizontale.
Si la droite est verticale, ce n'est pas une fonction affine. Son équation est de la forme x = c, où c est une constante.

Précautions

Utilisez une règle pour tracer la droite avec précision.
Vérifiez que les points utilisés sont exacts.
Assurez-vous que l'échelle des axes est appropriée.

Tableau de valeurs

Créez un tableau de valeurs. Choisissez quelques valeurs pour x. Calculez les valeurs correspondantes de f(x). Placez les points (x, f(x)) sur le graphique. Tracez la droite passant par ces points.

Utilisation d'un logiciel graphique

Utilisez un logiciel de tracé de courbes. Entrez l'équation de la fonction affine. Le logiciel tracera automatiquement la droite.

Droite et Inéquations

La représentation graphique permet de visualiser les solutions d'une inéquation affine. Par exemple, f(x) > 0 correspond à la partie de la droite située au-dessus de l'axe des abscisses.

Intersection de deux droites

L'intersection de deux droites représente la solution d'un système d'équations affines. Les coordonnées du point d'intersection sont les valeurs de x et y qui satisfont les deux équations. Trouvez le point d'intersection. Lisez ses coordonnées.

Coefficient directeur négatif

Une droite avec un coefficient directeur négatif descend de gauche à droite. Plus la valeur absolue du coefficient directeur est grande, plus la pente est forte.

Parallélisme et Perpendicularité

Deux droites sont parallèles si et seulement si elles ont le même coefficient directeur. Deux droites sont perpendiculaires si et seulement si le produit de leurs coefficients directeurs est égal à -1.

Résumé

La représentation graphique d'une fonction affine est essentielle. Comprendre les concepts de coefficient directeur et d'ordonnée à l'origine est primordial. Plusieurs méthodes permettent de tracer une droite. Le choix dépend des informations disponibles.