Comment Prouver Que Deux Droites Sont Perpendiculaires

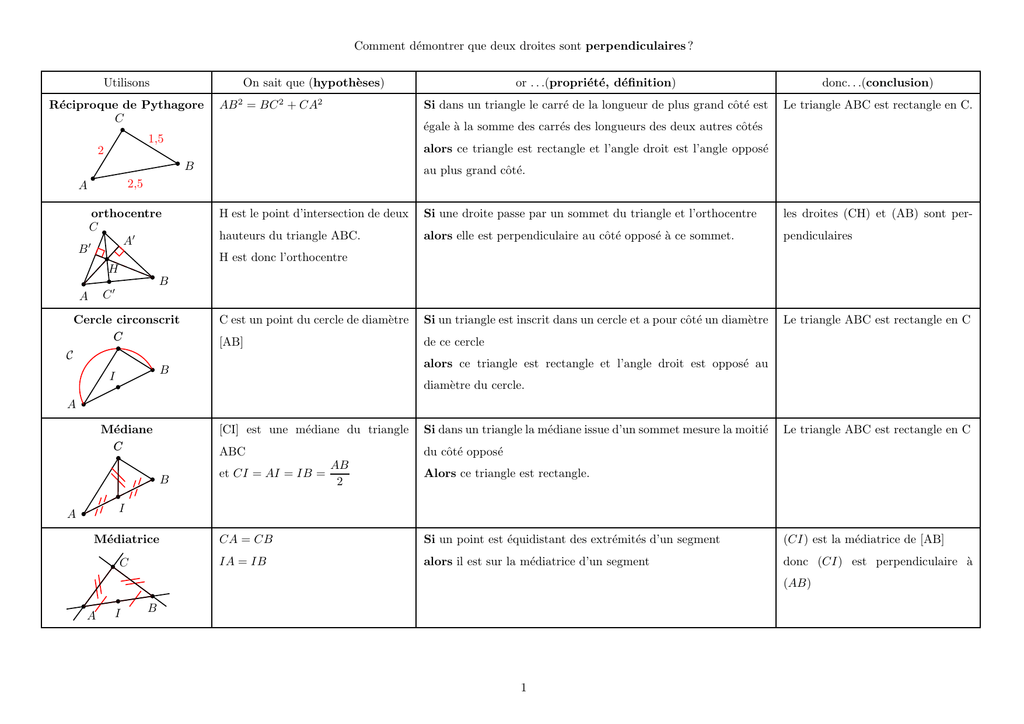
Pour démontrer que deux droites sont perpendiculaires, plusieurs méthodes s'offrent à vous. Chaque méthode repose sur des propriétés géométriques ou analytiques spécifiques. Le choix de la méthode dépend des informations dont vous disposez.

Une des méthodes les plus directes implique l'utilisation de la définition fondamentale de la perpendicularité. Si deux droites se coupent en formant un angle droit (90 degrés), alors elles sont perpendiculaires. Mesurez l'angle à l'intersection des deux droites. Utilisez un rapporteur ou une équerre. Si la mesure est de 90 degrés, les droites sont perpendiculaires.

Utilisation des Pentes

Dans un plan cartésien, les droites peuvent être définies par leurs équations. Une droite a une pente. Deux droites, d'équations respectives y = m₁x + b₁ et y = m₂x + b₂, sont perpendiculaires si et seulement si le produit de leurs pentes est égal à -1. C'est-à-dire, m₁ * m₂ = -1.

Identifiez les pentes des deux droites. Calculez le produit de ces pentes. Si le résultat est -1, les droites sont perpendiculaires.

Si l'équation d'une droite est donnée sous la forme ax + by + c = 0, la pente peut être calculée par m = -a/b. Déterminez les coefficients a et b pour chaque droite. Calculez les pentes correspondantes. Vérifiez si leur produit est égal à -1.

Utilisation du Théorème de Pythagore

Si vous connaissez les longueurs des côtés d'un triangle formé par les deux droites et un segment reliant les deux droites, vous pouvez utiliser le théorème de Pythagore. Si a² + b² = c², où a et b sont les longueurs des côtés adjacents à l'angle, et c est la longueur de l'hypoténuse (le côté opposé à l'angle), alors l'angle entre les deux droites est un angle droit. Les droites sont perpendiculaires.

Mesurez les longueurs des trois côtés du triangle. Vérifiez si le théorème de Pythagore est vérifié. Si l'équation est satisfaite, les droites sont perpendiculaires.

Utilisation des Vecteurs Directeurs

Les droites peuvent être définies par des vecteurs directeurs. Deux droites sont perpendiculaires si et seulement si le produit scalaire de leurs vecteurs directeurs est nul.

Déterminez les vecteurs directeurs des deux droites. Calculez le produit scalaire de ces vecteurs. Si le résultat est nul, les droites sont perpendiculaires.

Le produit scalaire de deux vecteurs u = (x₁, y₁) et v = (x₂, y₂) est donné par u.v = x₁x₂ + y₁y₂. Appliquez cette formule pour calculer le produit scalaire. Vérifiez si le résultat est nul.

Utilisation des Droites Parallèles et Perpendiculaires

Si vous savez qu'une droite est perpendiculaire à une autre droite, et qu'une troisième droite est parallèle à la première, alors la troisième droite est également perpendiculaire à la deuxième.

Identifiez la droite de référence et la droite qui lui est perpendiculaire. Déterminez si la troisième droite est parallèle à la droite de référence. Concluez que la troisième droite est perpendiculaire à la deuxième droite.

Démonstration Géométrique

Utilisez des constructions géométriques pour démontrer la perpendicularité. Construisez un cercle. Placez le centre du cercle sur l'intersection des deux droites. Si les points d'intersection des droites avec le cercle forment un diamètre, alors les droites sont perpendiculaires. Cela découle du théorème de l'angle inscrit.

Tracez le cercle. Identifiez les points d'intersection des droites avec le cercle. Vérifiez si ces points forment un diamètre du cercle.

Utilisation de la Géométrie Analytique Avancée

Des méthodes plus avancées, utilisant la géométrie analytique, peuvent également être employées. Ces méthodes impliquent souvent des transformations géométriques et des manipulations algébriques complexes.

Considérez l'application de transformations orthogonales. Analysez les propriétés invariantes sous ces transformations. Utilisez ces propriétés pour établir la perpendicularité.

Conclusion

Plusieurs approches permettent de prouver la perpendicularité de deux droites. La méthode la plus appropriée dépend des données disponibles et du contexte du problème. La maîtrise de ces différentes techniques est essentielle pour résoudre des problèmes de géométrie. Assurez-vous de comprendre les conditions d'application de chaque méthode. Une application correcte garantit une preuve rigoureuse.