Déterminer l'ensemble de définition d'une fonction est une étape cruciale pour comprendre son comportement et ses limites. C'est identifier toutes les valeurs pour lesquelles la fonction renvoie une valeur réelle. Aucune approximation n'est tolérée.
L'ensemble de définition, souvent noté Df, représente donc l'ensemble des abscisses pour lesquelles l'image par la fonction existe. Nous allons explorer en détail les méthodes pour le déterminer avec précision.
Fonctions Polynômes
Les fonctions polynômes, de la forme générale a_n*x^n + a_{n-1}x^{n-1} + ... + a_1x + a_0, où les a_i sont des constantes réelles, sont définies sur l'ensemble des nombres réels, noté ℝ. Il n'y a aucune restriction. Donc, Df = ℝ.
Fonctions Rationnelles
Une fonction rationnelle est un quotient de deux polynômes, P(x)/Q(x). L'ensemble de définition est l'ensemble des réels pour lesquels le dénominateur, Q(x), est non nul.
Résolvez l'équation Q(x) = 0. Les solutions de cette équation sont les valeurs à exclure de l'ensemble des réels. Df = ℝ \ {x | Q(x) = 0}. C'est-à-dire, l'ensemble des réels moins les racines de Q(x).
Fonctions avec Racines Carrées
Pour une fonction de la forme √(f(x)), l'expression sous la racine carrée, f(x), doit être positive ou nulle. On doit donc résoudre l'inéquation f(x) ≥ 0.
La résolution de cette inéquation détermine l'ensemble de définition. Df = {x | f(x) ≥ 0}. Cela peut nécessiter l'utilisation d'un tableau de signes pour déterminer les intervalles où f(x) est positive ou nulle.
Fonctions Logarithmes
Pour une fonction de la forme ln(f(x)) ou log(f(x)), l'expression à l'intérieur du logarithme, f(x), doit être strictement positive. On résout donc l'inéquation f(x) > 0.
La résolution de cette inéquation définit l'ensemble de définition. Df = {x | f(x) > 0}. L'égalité à zéro est exclue.
Fonctions Tangente
La fonction tangente, tan(x) = sin(x)/cos(x), est définie partout sauf là où cos(x) = 0.
Cos(x) = 0 lorsque x = π/2 + kπ, où k est un entier relatif. Donc, Df = ℝ \ {π/2 + kπ | k ∈ ℤ}.
Fonctions Arcsinus et Arccosinus
La fonction arcsinus, arcsin(x), est définie pour -1 ≤ x ≤ 1. Donc Df = [-1, 1].
La fonction arccosinus, arccos(x), est également définie pour -1 ≤ x ≤ 1. Donc Df = [-1, 1].
Combinaison de Fonctions
Si une fonction est une combinaison de plusieurs types de fonctions, l'ensemble de définition est l'intersection des ensembles de définition de chaque composante.
Par exemple, si f(x) = √(g(x)) + ln(h(x)), alors Df = {x | g(x) ≥ 0} ∩ {x | h(x) > 0}. Il faut donc résoudre chaque condition séparément et identifier l'intersection des solutions.
Exemples Concrets
Soit f(x) = √(x - 2) / (x - 5). La racine carrée impose x - 2 ≥ 0, donc x ≥ 2. Le dénominateur impose x - 5 ≠ 0, donc x ≠ 5. L'ensemble de définition est donc [2, 5) ∪ (5, +∞).
Soit g(x) = ln(x² - 4). Le logarithme impose x² - 4 > 0. Factorisation donne (x - 2)(x + 2) > 0. Un tableau de signes montre que x < -2 ou x > 2. Donc, Dg = (-∞, -2) ∪ (2, +∞).
Importance de la Rigueur
La détermination de l'ensemble de définition nécessite une rigueur absolue. Une erreur, même mineure, peut conduire à une interprétation incorrecte du comportement de la fonction.
Il est impératif de vérifier chaque condition et de s'assurer que l'ensemble de définition est exprimé correctement. L'utilisation d'un tableau de signes est fortement recommandée pour les inéquations.
Conclusion
La maîtrise de la détermination de l'ensemble de définition est une compétence fondamentale en analyse mathématique. Une compréhension approfondie des différents types de fonctions et des restrictions qu'elles imposent est essentielle. En suivant les méthodes décrites ci-dessus avec précision, vous serez en mesure de déterminer l'ensemble de définition de n'importe quelle fonction avec assurance. Une application méticuleuse des règles permet une analyse correcte et prévient les erreurs d'interprétation.
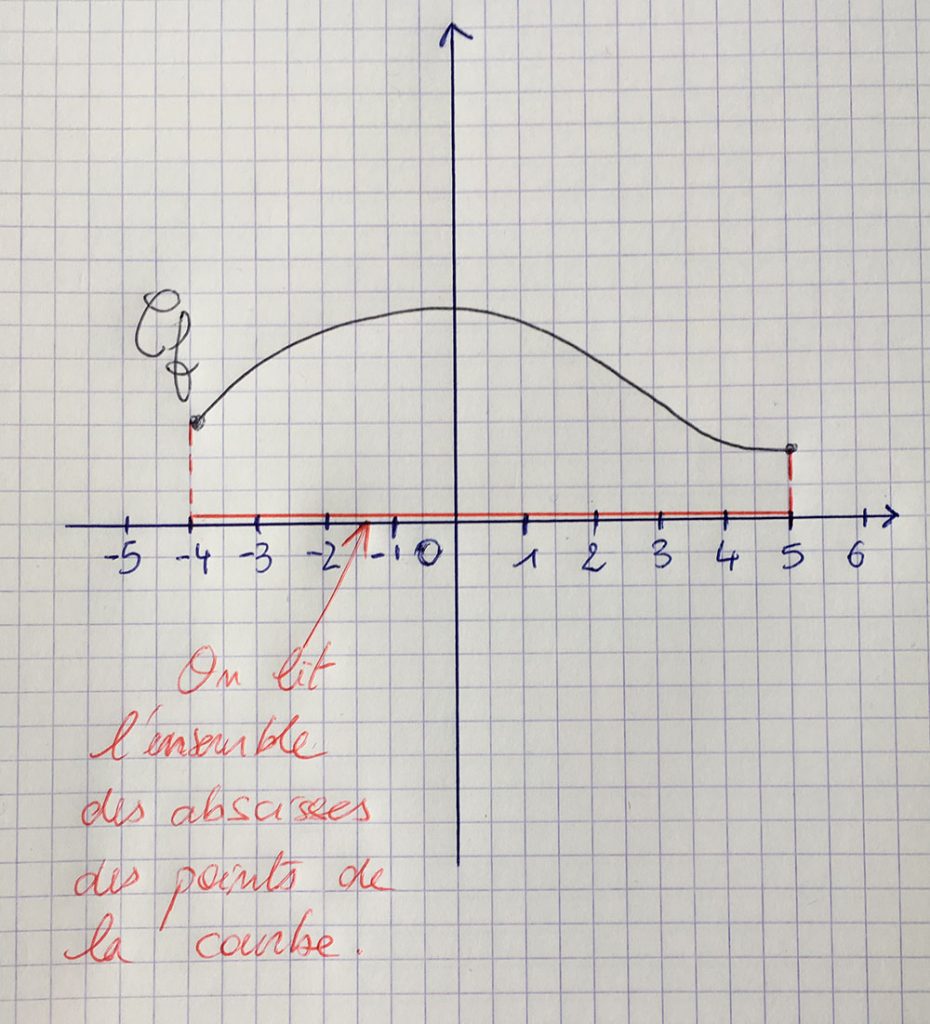
49 La courbe suivante représente une fonction f. 1. Préciser l'ensemble
-
comment déterminer l'ensemble de définition d'une fonction
-
comment déterminer l'ensemble de dérivabilité d'une fonction
-
comment déterminer l'ensemble de définition
-
comment déterminer l'ensemble de définition d'une fonction rationnelle
-
comment déterminer l'ensemble de validité
-
comment déterminer l'ensemble de définition de f
-
comment déterminer l'ensemble des points d'un nombre complexe
-
comment déterminer l'ensemble de définition d'une fonction exponentielle
-
comment déterminer l'ensemble de dérivabilité
-
comment déterminer l'ensemble des points m d'affixe z