Un quadrilatère est un parallélogramme si ses côtés opposés sont parallèles deux à deux. Vérifiez cette condition en calculant les pentes des côtés. Si les pentes des côtés opposés sont égales, alors ces côtés sont parallèles.
Une autre méthode consiste à démontrer que les côtés opposés sont de même longueur. Calculez les longueurs des côtés opposés. Utilisez la formule de distance entre deux points. Si les longueurs sont égales, les côtés opposés sont congruents.
Vous pouvez aussi prouver que deux côtés opposés sont parallèles et de même longueur. Calculez la pente et la longueur d'une paire de côtés opposés. Si la pente est la même et la longueur est la même, le quadrilatère est un parallélogramme.
Démontrez que les angles opposés sont égaux deux à deux. Calculez les mesures des angles opposés. Si les angles opposés ont la même mesure, c'est un parallélogramme.
Prouvez que les angles consécutifs sont supplémentaires. Additionnez les mesures des angles consécutifs. Si la somme est de 180 degrés, les angles sont supplémentaires.
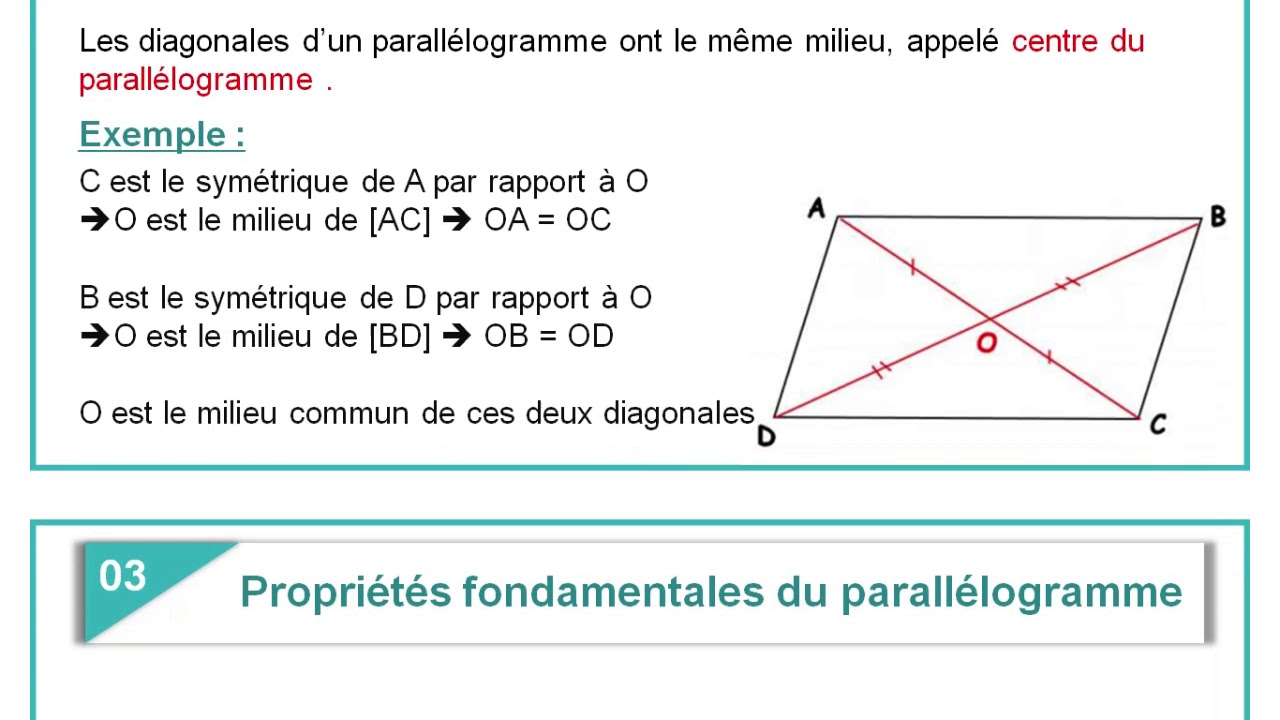
Si les diagonales se coupent en leur milieu, le quadrilatère est un parallélogramme. Déterminez les coordonnées du point milieu de chaque diagonale. Utilisez la formule du point milieu. Si les deux points milieux coïncident, les diagonales se coupent en leur milieu.
Calcul des Pentes
Soient A(x₁, y₁) et B(x₂, y₂) deux sommets. La pente du segment AB est (y₂ - y₁) / (x₂ - x₁).
Calcul des Distances
La distance entre les points A(x₁, y₁) et B(x₂, y₂) est √((x₂ - x₁)² + (y₂ - y₁)²)
Calcul du Point Milieu
Le point milieu du segment AB, où A(x₁, y₁) et B(x₂, y₂), a pour coordonnées ((x₁ + x₂) / 2, (y₁ + y₂) / 2).
Utilisation des Vecteurs
Vous pouvez utiliser des vecteurs. Soient les sommets A, B, C et D. Calculez les vecteurs AB et DC. Si AB = DC, alors ABCD est un parallélogramme. Calculez également les vecteurs AD et BC. Si AD = BC, cela confirme que ABCD est un parallélogramme.
Vérifiez que AB est parallèle à DC en montrant que AB = kDC, où k est un scalaire. De même, vérifiez que AD est parallèle à BC en montrant que AD = lBC, où l est un scalaire.
Démonstration par Translation
Considérez une translation qui envoie A sur B. Si cette translation envoie également D sur C, alors le quadrilatère ABCD est un parallélogramme. Cela équivaut à montrer que AB = DC en termes de vecteurs.
Utilisation des Transformations
Appliquez une rotation de 180 degrés autour du centre du quadrilatère. Si l'image du quadrilatère coïncide avec le quadrilatère original, c'est un parallélogramme. Le centre du quadrilatère serait le point d'intersection des diagonales.
Contre-Exemples
Pour prouver qu'un quadrilatère n'est PAS un parallélogramme, il suffit de démontrer qu'UNE SEULE des conditions ci-dessus n'est pas vérifiée. Par exemple, si un seul couple de côtés opposés n'est pas parallèle ou n'est pas de même longueur, ce n'est pas un parallélogramme.
Cas Particuliers
Un rectangle, un losange et un carré sont des parallélogrammes. Pour identifier ces cas particuliers, vérifiez des conditions supplémentaires. Un rectangle a quatre angles droits. Un losange a quatre côtés de même longueur. Un carré a quatre angles droits et quatre côtés de même longueur.
Exemple concret
Soient les points A(1, 1), B(4, 2), C(5, 5) et D(2, 4). Calculons les pentes des côtés opposés.
Pente de AB = (2-1)/(4-1) = 1/3 Pente de DC = (5-4)/(5-2) = 1/3 Pente de AD = (4-1)/(2-1) = 3 Pente de BC = (5-2)/(5-4) = 3
Les côtés AB et DC ont la même pente, donc ils sont parallèles. Les côtés AD et BC ont la même pente, donc ils sont parallèles. Donc, ABCD est un parallélogramme.
Calculons les longueurs des côtés. AB = sqrt((4-1)^2 + (2-1)^2) = sqrt(10) DC = sqrt((5-2)^2 + (5-4)^2) = sqrt(10) AD = sqrt((2-1)^2 + (4-1)^2) = sqrt(10) BC = sqrt((5-4)^2 + (5-2)^2) = sqrt(10)
Dans cet exemple spécifique, tous les côtés ont la même longueur. Cela indique que c'est un losange. On devrait vérifier que les angles ne sont pas droits pour confirmer que ce n'est pas un carré.
Remarques Importantes
Choisissez la méthode la plus appropriée en fonction des informations disponibles. Certaines méthodes peuvent être plus simples à appliquer que d'autres, selon les coordonnées des sommets ou les mesures des angles données. La clarté et la rigueur sont essentielles dans votre démonstration. Indiquez clairement les étapes suivies et justifiez chaque conclusion.
5G4 - 2 : Montrer qu'un quadrilatère est un parallélogramme - YouTube
-
comment démontrer qu'un quadrilatère est un parallélogramme
-
comment démontrer qu'un quadrilatère est un rectangle
-
comment démontrer qu'un quadrilatère est un losange
-
comment démontrer qu'un quadrilatère est un parallélogramme dans un repère orthonormé
-
comment démontrer qu'un quadrilatère est un carré
-
comment démontrer qu'un quadrilatère est un carré avec les vecteurs
-
comment démontrer qu'un quadrilatère est un trapèze
-
comment démontrer qu'un quadrilatère est un parallélogramme avec les vecteurs
-
comment démontrer qu'un quadrilatère est un trapèze rectangle
-
comment démontrer qu'un quadrilatère est un trapèze avec les vecteurs