Comment Calculer Le Perimetre D Un Triangle Rectangle

Calculer le périmètre d'un triangle rectangle est une compétence fondamentale en géométrie. Plusieurs méthodes s'offrent à vous, chacune adaptée aux informations dont vous disposez. Explorons en détail ces différentes approches.

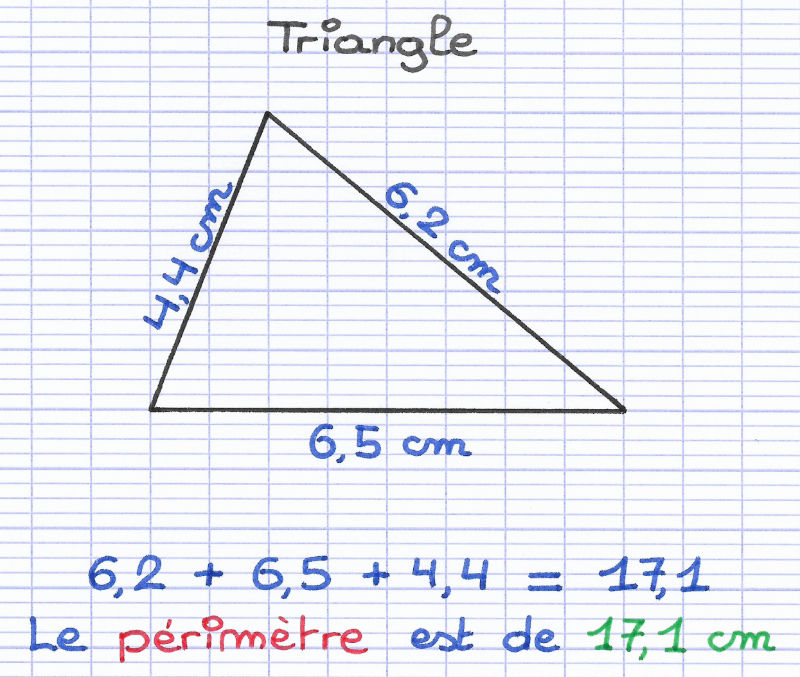
La méthode la plus directe exige la connaissance des longueurs des trois côtés du triangle. Additionnez simplement la longueur de chaque côté. La formule est la suivante : Périmètre (P) = a + b + c, où 'a', 'b' et 'c' représentent les longueurs des côtés.

Utilisation du théorème de Pythagore

Le théorème de Pythagore s'avère indispensable si vous ne connaissez que deux côtés du triangle rectangle. Ce théorème stipule que dans un triangle rectangle, le carré de la longueur de l'hypoténuse (le côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des deux autres côtés (les cathètes).

La formule est : a² + b² = c², où 'c' est l'hypoténuse et 'a' et 'b' sont les cathètes.

Si vous connaissez les longueurs des deux cathètes (a et b), calculez l'hypoténuse (c) : c = √(a² + b²). Une fois l'hypoténuse calculée, additionnez les trois côtés pour obtenir le périmètre : P = a + b + c.

Si vous connaissez l'hypoténuse (c) et une cathète (par exemple, a), calculez l'autre cathète (b) : b = √(c² - a²). Ensuite, calculez le périmètre : P = a + b + c.

Utilisation des fonctions trigonométriques

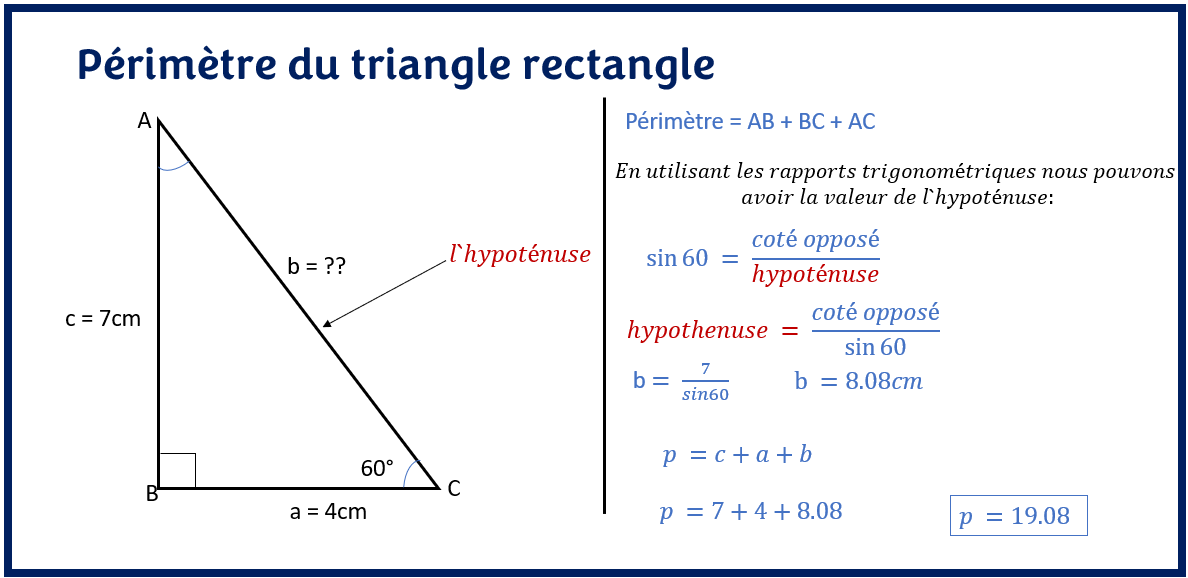
Les fonctions trigonométriques, telles que le sinus, le cosinus et la tangente, deviennent utiles lorsque vous connaissez un angle aigu (autre que l'angle droit) et la longueur d'un côté du triangle.

Si vous connaissez un angle aigu (θ) et l'hypoténuse (c), vous pouvez calculer les cathètes (a et b) :

a = c * sin(θ)
b = c * cos(θ)

Calculez ensuite le périmètre : P = a + b + c.

Si vous connaissez un angle aigu (θ) et une cathète (par exemple, a), vous pouvez calculer l'autre cathète (b) et l'hypoténuse (c) :

b = a / tan(θ)
c = a / sin(θ)

Calculez ensuite le périmètre : P = a + b + c.

Exemples Concrets

Considérons un triangle rectangle dont les cathètes mesurent 3 cm et 4 cm. Appliquez le théorème de Pythagore pour trouver l'hypoténuse : c = √(3² + 4²) = √(9 + 16) = √25 = 5 cm. Le périmètre est donc : P = 3 + 4 + 5 = 12 cm.

Prenons un autre exemple. Vous connaissez l'hypoténuse (10 cm) et un angle aigu (30 degrés). Calculez les cathètes : a = 10 * sin(30°) = 10 * 0.5 = 5 cm et b = 10 * cos(30°) ≈ 10 * 0.866 ≈ 8.66 cm. Le périmètre est approximativement : P = 5 + 8.66 + 10 ≈ 23.66 cm.

Précision et Unités

Soyez rigoureux avec les unités de mesure. Tous les côtés doivent être exprimés dans la même unité (par exemple, centimètres, mètres, pouces) avant de procéder au calcul du périmètre. Le résultat final sera exprimé dans la même unité.

L'utilisation d'une calculatrice scientifique est recommandée pour les calculs trigonométriques et les racines carrées, garantissant ainsi une plus grande précision. Arrondissez les résultats intermédiaires et finaux selon le degré de précision requis.

En résumé, le calcul du périmètre d'un triangle rectangle dépend de l'information disponible. Le théorème de Pythagore et les fonctions trigonométriques sont des outils essentiels pour déduire les longueurs manquantes. L'addition des trois côtés, une fois connus, vous donnera le périmètre exact. N'oubliez pas la cohérence des unités et l'importance de la précision dans vos calculs.