Comment Calculer Le Volume D'une Pyramide A Base Triangulaire

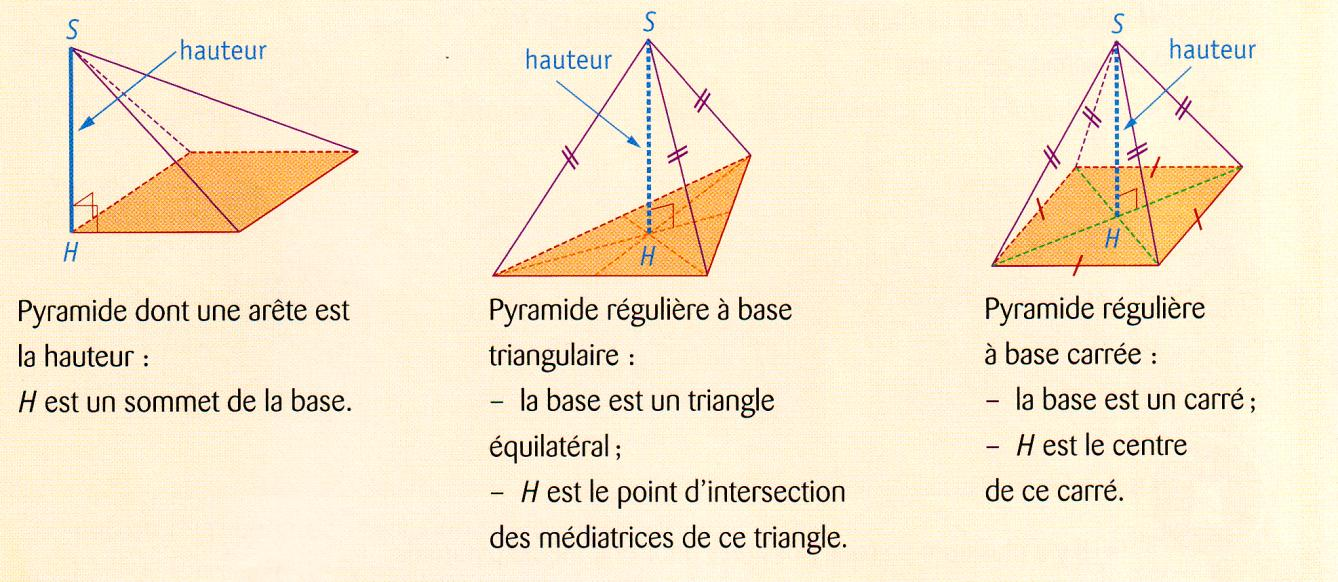
Dans le domaine fascinant de la géométrie, la pyramide à base triangulaire, ou tétraèdre, occupe une place de choix. Sa simplicité apparente dissimule une richesse mathématique qui mérite d'être explorée. Nous allons disséquer le processus de calcul de son volume avec une précision inégalée.

La formule fondamentale est votre point de départ. Elle se présente ainsi :

V = (1/3) * Aire de la base * Hauteur

L'aire de la base triangulaire est primordiale. Plusieurs méthodes s'offrent à vous, selon les informations dont vous disposez.

Si vous connaissez la base (b) et la hauteur (h) du triangle, appliquez :

Aire = (1/2) * b * h

Si les trois côtés (a, b, c) du triangle sont connus, la formule de Héron devient votre alliée. Calculez d'abord le demi-périmètre (s) :

s = (a + b + c) / 2

Puis, l'aire :

Aire = √(s * (s - a) * (s - b) * (s - c))

Enfin, si vous connaissez deux côtés (a, b) et l'angle (γ) entre eux, utilisez :

Aire = (1/2) * a * b * sin(γ)

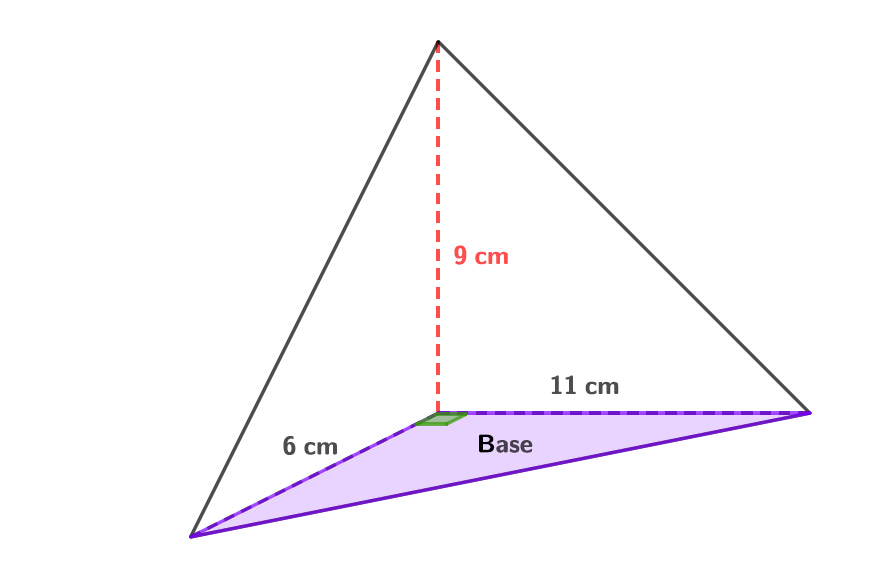
La hauteur de la pyramide est la distance perpendiculaire entre le sommet et la base. Sa mesure est essentielle pour le calcul du volume.

Une fois l'aire de la base et la hauteur de la pyramide déterminées, vous êtes prêt à calculer le volume.

Multipliez l'aire de la base par la hauteur de la pyramide.

Divisez le résultat par trois.

Le résultat obtenu est le volume de la pyramide. Il est exprimé en unités cubiques (cm³, m³, etc.).

Exemple Concret

Considérons une pyramide à base triangulaire. Sa base a une base de 6 cm et une hauteur de 4 cm. La hauteur de la pyramide est de 10 cm.

Calculons l'aire de la base triangulaire :

Aire = (1/2) * 6 cm * 4 cm = 12 cm²

Calculons le volume de la pyramide :

V = (1/3) * 12 cm² * 10 cm = 40 cm³

Le volume de cette pyramide est donc de 40 cm³.

Cas Particuliers et Précautions

Pour un tétraèdre régulier, dont toutes les faces sont des triangles équilatéraux identiques, une formule simplifiée existe. Si 'a' est la longueur d'une arête :

V = (a³ * √2) / 12

Soyez extrêmement vigilant quant aux unités de mesure. Une conversion incorrecte peut fausser le résultat final.

Assurez-vous que la hauteur de la pyramide est bien perpendiculaire à la base. Une mesure oblique conduira à un volume incorrect.

Dans des problèmes complexes, il peut être nécessaire d'utiliser des notions de trigonométrie pour déterminer la hauteur de la pyramide ou l'aire de la base.

La maîtrise du calcul du volume d'une pyramide à base triangulaire ouvre la porte à une compréhension plus profonde de la géométrie tridimensionnelle. Sa rigueur et sa précision en font un outil indispensable pour les mathématiciens, les ingénieurs et les architectes.