Comment Calculer L'aire D'un Quadrilatère Irrégulier

Voici une exploration détaillée du calcul de l'aire d'un quadrilatère irrégulier.

Un quadrilatère irrégulier ne possède pas de propriétés spécifiques comme le carré ou le rectangle. Ses côtés et ses angles sont de longueurs variables. Plusieurs méthodes permettent de calculer son aire.

Décomposition en triangles

C'est une méthode largement applicable. Divisez le quadrilatère en deux triangles. Tracez une diagonale. Calculez l'aire de chaque triangle. Additionnez les aires obtenues.

Pour calculer l'aire d'un triangle, plusieurs options s'offrent à vous :

Connaissant la base et la hauteur : Appliquez la formule Aire = (1/2) * base * hauteur. La hauteur doit être perpendiculaire à la base.
Connaissant deux côtés et l'angle inclus : Utilisez la formule Aire = (1/2) * a * b * sin(C). a et b sont les longueurs des côtés. C est l'angle entre ces côtés.
Connaissant les trois côtés : Employez la formule de Héron. Soit s le demi-périmètre du triangle : s = (a + b + c) / 2. L'aire est alors Aire = √(s * (s - a) * (s - b) * (s - c)). a, b, et c sont les longueurs des côtés.

Formule de Brahmagupta

Cette formule s'applique aux quadrilatères cycliques. Un quadrilatère cyclique est inscriptible dans un cercle. Soit a, b, c, et d les longueurs des côtés. Soit s le demi-périmètre : s = (a + b + c + d) / 2. L'aire est alors Aire = √((s - a) * (s - b) * (s - c) * (s - d)).

Attention, cette formule ne fonctionne que pour les quadrilatères cycliques.

Formule de Bretschneider

C'est la formule la plus générale. Elle s'applique à tout quadrilatère. Soit a, b, c, et d les longueurs des côtés. Soit α et γ deux angles opposés. Soit s le demi-périmètre : s = (a + b + c + d) / 2. L'aire est donnée par: Aire = √((s - a) * (s - b) * (s - c) * (s - d) - a * b * c * d * cos²((α + γ) / 2)).

Cette formule nécessite la connaissance des quatre côtés et de deux angles opposés.

Utilisation des coordonnées

Si vous connaissez les coordonnées des quatre sommets du quadrilatère, vous pouvez utiliser la formule suivante (aussi connue sous le nom de formule du lacet). Soient les sommets (x1, y1), (x2, y2), (x3, y3), et (x4, y4).

Aire = (1/2) * |(x1y2 + x2y3 + x3y4 + x4y1) - (x2y1 + x3y2 + x4y3 + x1y4)|

Cette formule fonctionne pour n'importe quel quadrilatère, qu'il soit convexe ou concave. L'ordre des sommets est important. Ils doivent être pris dans le sens anti-horaire (ou horaire). La valeur absolue garantit une aire positive.

Méthodes Approximatives

Si une grande précision n'est pas requise, des approximations peuvent être utilisées.

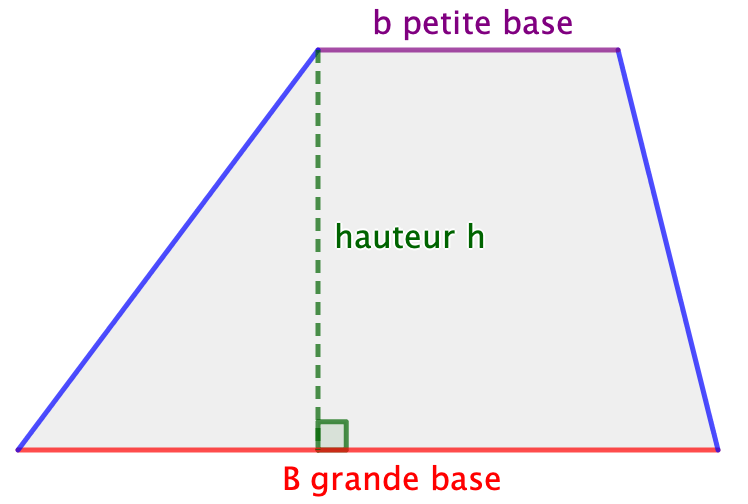
Diviser en trapèzes: Divisez le quadrilatère en trapèzes. Calculez l'aire de chaque trapèze. Additionnez les aires. L'aire d'un trapèze est Aire = (1/2) * (base1 + base2) * hauteur.
Estimation visuelle: Superposez une grille sur le quadrilatère. Comptez les carrés complets et les carrés partiels. Estimez l'aire totale. Cette méthode est très approximative.

Conseils Pratiques

Vérifiez vos unités. Toutes les longueurs doivent être dans la même unité. L'aire sera dans l'unité au carré.
Dessinez un schéma. Cela aide à visualiser le problème. Cela facilite l'identification des bases, hauteurs, et angles.
Choisissez la méthode appropriée. Considérez les informations dont vous disposez. La formule de Bretschneider est la plus générale. La décomposition en triangles est souvent la plus simple.
Utilisez une calculatrice. Simplifiez les calculs. Evitez les erreurs.

En conclusion, calculer l'aire d'un quadrilatère irrégulier exige de choisir la méthode adaptée aux informations disponibles. La décomposition en triangles reste une approche fondamentale. La formule de Bretschneider offre une solution générale, tandis que la formule des coordonnées est particulièrement utile si les sommets sont définis dans un plan.