Comment Calculer La Hauteur D'un Triangle Sans Connaitre L'aire

Pour calculer la hauteur d'un triangle sans connaître son aire, plusieurs méthodes existent. Elles dépendent des informations dont vous disposez sur le triangle.

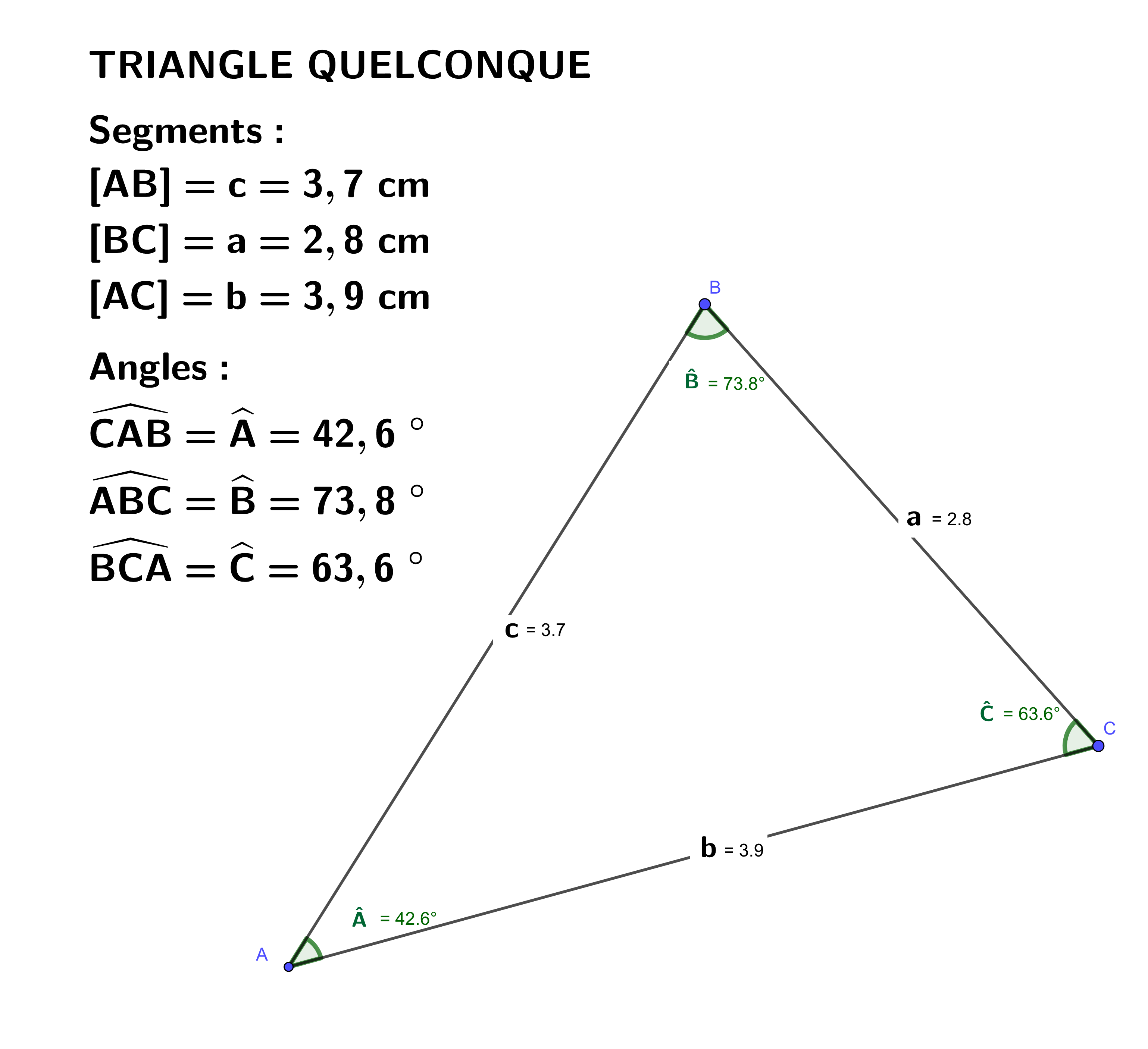
Si vous connaissez les longueurs des trois côtés (a, b, c), vous pouvez utiliser la formule de Héron. Calculez d'abord le demi-périmètre (s):

s = (a + b + c) / 2

Calculez ensuite l'aire (A) du triangle :

A = √(s(s - a)(s - b)(s - c))

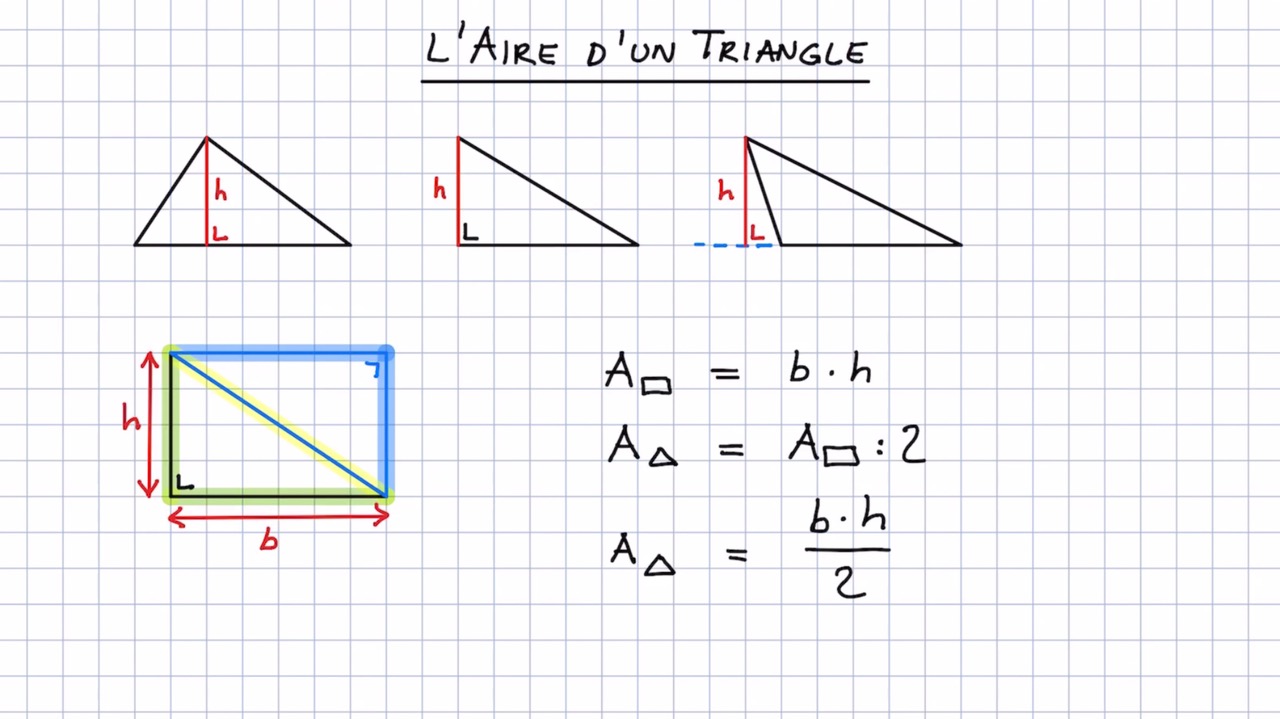
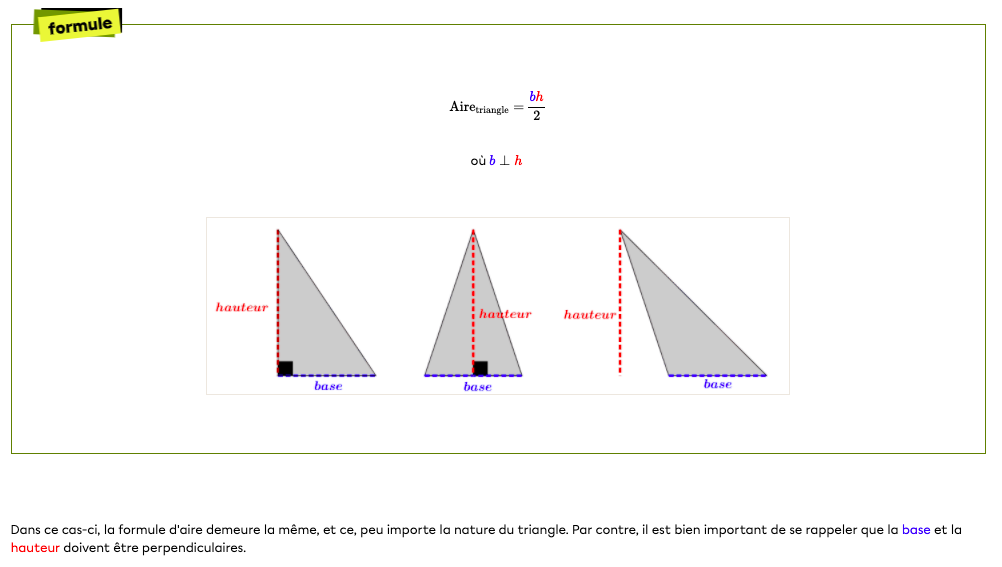
Une fois l'aire (A) calculée, vous pouvez déterminer la hauteur (h) relative à un côté spécifique (par exemple, le côté b) :

h = (2 * A) / b

Vous obtiendrez ainsi la hauteur relative au côté b. Répétez l'opération pour les autres côtés si nécessaire.

Si vous connaissez deux côtés (a et b) et l'angle (γ) entre eux, vous pouvez utiliser la formule suivante pour l'aire :

A = (1/2) * a * b * sin(γ)

Ensuite, comme précédemment, si vous souhaitez trouver la hauteur (h) relative au côté a, vous utiliserez :

h = (2 * A) / a

Si vous connaissez un angle et un côté adjacent à cet angle, mais pas l'aire, d'autres approches sont nécessaires.

Si vous avez un triangle rectangle et que vous connaissez les longueurs de deux côtés, vous pouvez utiliser le théorème de Pythagore.

Si l'hypoténuse (c) est connue, ainsi qu'un côté (a), alors le troisième côté (b), qui peut servir de hauteur si 'a' est considéré comme la base, se calcule :

b = √(c² - a²)

Si vous connaissez un angle (α) et le côté opposé à cet angle (a), et que vous souhaitez trouver la hauteur relative à un autre côté, la trigonométrie peut être utilisée. Il faut connaître au moins un autre élément du triangle (un autre angle ou un autre côté).

Imaginez que vous connaissez l'angle α et le côté a opposé. Vous connaissez également l'angle β. Vous pouvez alors trouver l'angle γ :

γ = 180° - α - β

Ensuite, utilisez la loi des sinus pour trouver le côté b :

b / sin(β) = a / sin(α) b = (a * sin(β)) / sin(α)

Maintenant que vous connaissez b, vous pouvez calculer la hauteur (h) relative au côté a:

h = b * sin(γ)

Si le triangle est isocèle, deux côtés sont égaux. Cela simplifie certains calculs. Si vous connaissez la base et l'un des côtés égaux, vous pouvez tracer une hauteur à partir du sommet opposé à la base. Cette hauteur divisera la base en deux parties égales. Vous pouvez alors utiliser le théorème de Pythagore pour calculer la hauteur.

Soit la base 'b' et le côté isocèle 'a'. La hauteur 'h' est alors :

h = √(a² - (b/2)²)

Si vous disposez des coordonnées des trois sommets du triangle (x1, y1), (x2, y2) et (x3, y3), vous pouvez utiliser la formule de l'aire basée sur les coordonnées :

A = (1/2) |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|

Puis, si vous connaissez la longueur d'un des côtés (par exemple, le côté entre (x1, y1) et (x2, y2)), vous pouvez calculer cette longueur 'b' avec la formule de distance :

b = √((x2 - x1)² + (y2 - y1)²)

Et enfin, la hauteur 'h' relative à ce côté 'b' est :

h = (2 * A) / b

La géométrie analytique offre une autre perspective.

Si le triangle est à l'intérieur d'un cercle circonscrit et vous connaissez le rayon (R) du cercle circonscrit et les longueurs des côtés, vous pouvez utiliser la formule :

A = (abc) / (4R)

Une fois l'aire (A) déterminée, vous pourrez utiliser les méthodes déjà décrites pour trouver la hauteur.

Dans certains cas, vous pourriez avoir des informations sur les médianes du triangle. Les médianes sont les segments de droite reliant un sommet au milieu du côté opposé. Si vous connaissez les longueurs des trois médianes (ma, mb, mc), vous pouvez calculer l'aire du triangle. Cette aire peut ensuite être utilisée pour trouver la hauteur. La formule de l'aire en fonction des médianes est complexe, mais elle existe. Une fois l'aire trouvée, vous pourrez calculer les hauteurs.

Si vous connaissez l'aire et un angle, cela ne suffit pas pour calculer la hauteur directement. Vous aurez besoin d'informations supplémentaires sur les côtés adjacents à cet angle.

Il est crucial de bien identifier les informations dont vous disposez pour choisir la méthode la plus appropriée pour calculer la hauteur d'un triangle sans connaître son aire au départ. Chaque méthode exploite des relations géométriques et trigonométriques spécifiques.