Ah, le rectangle. Une figure géométrique simple en apparence, mais recelant des secrets de calcul insoupçonnés. Bien que le théorème de Pythagore soit l'outil le plus communément associé au calcul de sa diagonale, il existe bel et bien des approches alternatives, moins directes certes, mais d'une élégance conceptuelle certaine. Découvrons ensemble comment aborder ce défi sans recourir à la célèbre relation a² + b² = c².
Commençons par établir un cadre. Nous savons que le rectangle possède des angles droits. Sa diagonale le divise en deux triangles rectangles identiques. C'est cette propriété qui justifie l'emploi fréquent de Pythagore. Cependant, imaginez que l'on vous fournisse des informations différentes, peut-être l'aire du rectangle et un rapport entre ses côtés, ou encore des relations angulaires impliquant sa diagonale. C'est dans ces situations que les méthodes alternatives prennent tout leur sens.
Exploitation des Relations Trigonométriques
Sans Pythagore, la trigonométrie est une alliée précieuse. Si l'on connaît l'angle qu'une diagonale forme avec l'un des côtés du rectangle (appelons cet angle θ), ainsi que la longueur de ce côté (par exemple, la largeur l), on peut utiliser la fonction cosinus ou sinus pour déterminer la longueur de la diagonale (d).
Rappelons les définitions :
- cos(θ) = côté adjacent / hypoténuse
- sin(θ) = côté opposé / hypoténuse
Dans notre rectangle, l'hypoténuse est la diagonale. Donc :
- cos(θ) = l / d => d = l / cos(θ)
- sin(θ) = L / d => d = L / sin(θ) (où L est la longueur du rectangle)
Ainsi, si vous connaissez la largeur (l) et l'angle θ, vous pouvez calculer la diagonale directement. Si vous connaissez la longueur (L) et l'angle θ, vous pouvez également la calculer.
Utilisation de l'Aire et du Rapport des Côtés
Supposons maintenant que l'on vous donne l'aire du rectangle (A) et le rapport entre sa longueur et sa largeur, par exemple L = k * l (où k est une constante). L'aire du rectangle est donnée par A = L * l.
On peut alors substituer L par k * l dans l'équation de l'aire :
A = (k * l) * l = k * l²
On en déduit la largeur :
l = √( A / k )
Et ensuite la longueur :
L = k * √( A / k ) = √( k * A )
Maintenant, nous pourrions être tentés d'utiliser Pythagore pour trouver d. Évitons cela. Concentrons-nous sur d'autres relations. Malheureusement, sans Pythagore direct, l'utilisation de l'aire et du rapport des côtés pour calculer directement la diagonale devient excessivement complexe et peu pratique. Il est plus simple, une fois L et l obtenus, de revenir à une approche trigonométrique si un angle est connu, même indirectement.
Approches Géométriques et Transformations
Une approche plus conceptuelle consiste à considérer le rectangle comme une transformation d'un carré. Imaginez un carré de côté l. En étirant ce carré dans une direction, on obtient un rectangle. L'étude de la déformation des diagonales pourrait, théoriquement, mener à une relation, mais elle serait hautement dépendante de paramètres de transformation spécifiques et difficilement généralisable. Cette méthode reste plus un exercice de pensée qu'une technique de calcul pratique.
Résolution de Problèmes Spécifiques
Dans certains problèmes très spécifiques, des relations géométriques particulières peuvent se révéler utiles. Par exemple, si l'on connaît l'aire de certains triangles formés par la diagonale et des points spécifiques situés sur les côtés du rectangle, on pourrait établir des relations entre les longueurs des côtés et, par conséquent, de la diagonale. Cependant, ces solutions sont hautement contextuelles et ne constituent pas une méthode générale.
En conclusion, bien que le théorème de Pythagore reste la méthode la plus efficace et la plus directe pour calculer la diagonale d'un rectangle, des alternatives existent. La trigonométrie, l'exploitation de l'aire et du rapport des côtés (combinée à des informations angulaires), et des considérations géométriques spécifiques peuvent permettre de résoudre ce problème sans recourir à a² + b² = c². Toutefois, il est crucial de noter que ces alternatives nécessitent des informations supplémentaires sur le rectangle, et leur application peut être plus complexe et moins intuitive que l'utilisation du théorème de Pythagore. Le choix de la méthode dépendra donc des données dont vous disposez et de votre familiarité avec les concepts mathématiques impliqués.
calcul d'une diagonale d'un rectangle 5ème Mathématiques
-
comment calculer la diagonale d'un rectangle
-
comment calculer la diagonale d'un carré
-
comment calculer la diagonale d'un rectangle sans pythagore
-
comment calculer la diagonale d'un triangle rectangle
-
comment calculer la diagonale d'un triangle
-
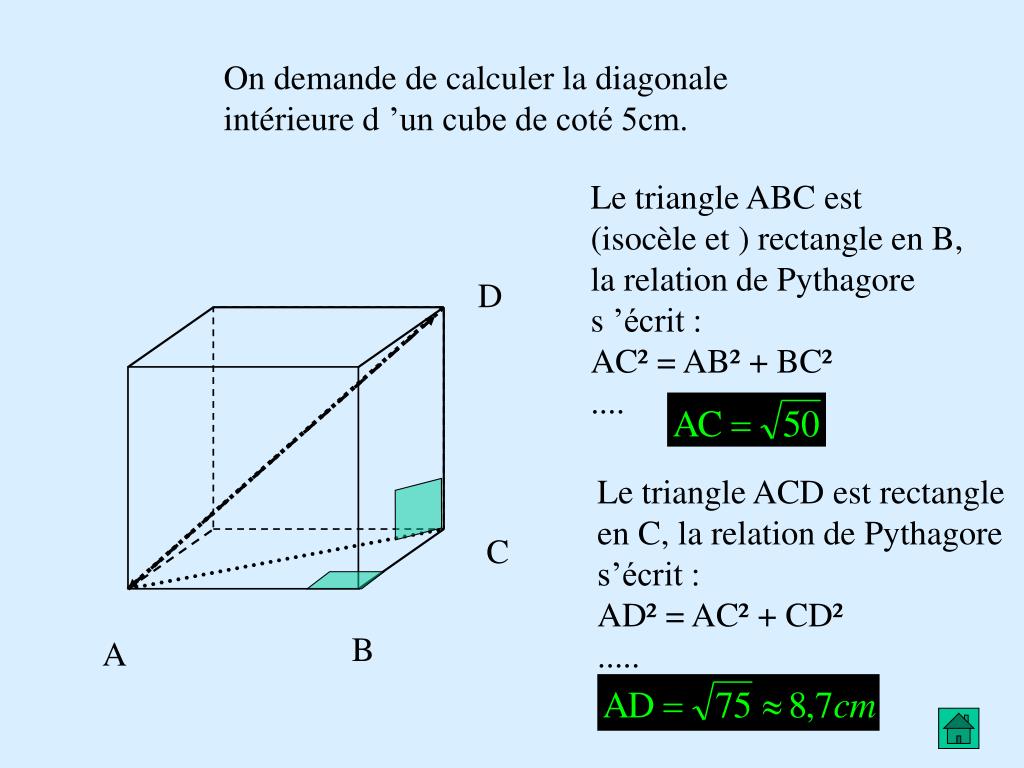
comment calculer la diagonale d'un cube
-
comment calculer la diagonale
-
comment calculer la diagonale d'un parallélogramme
-
comment calculer la diagonale d'un losange
-
comment calculer la diagonale d'un écran