Expression Vectorielle De La Force D'interaction Gravitationnelle

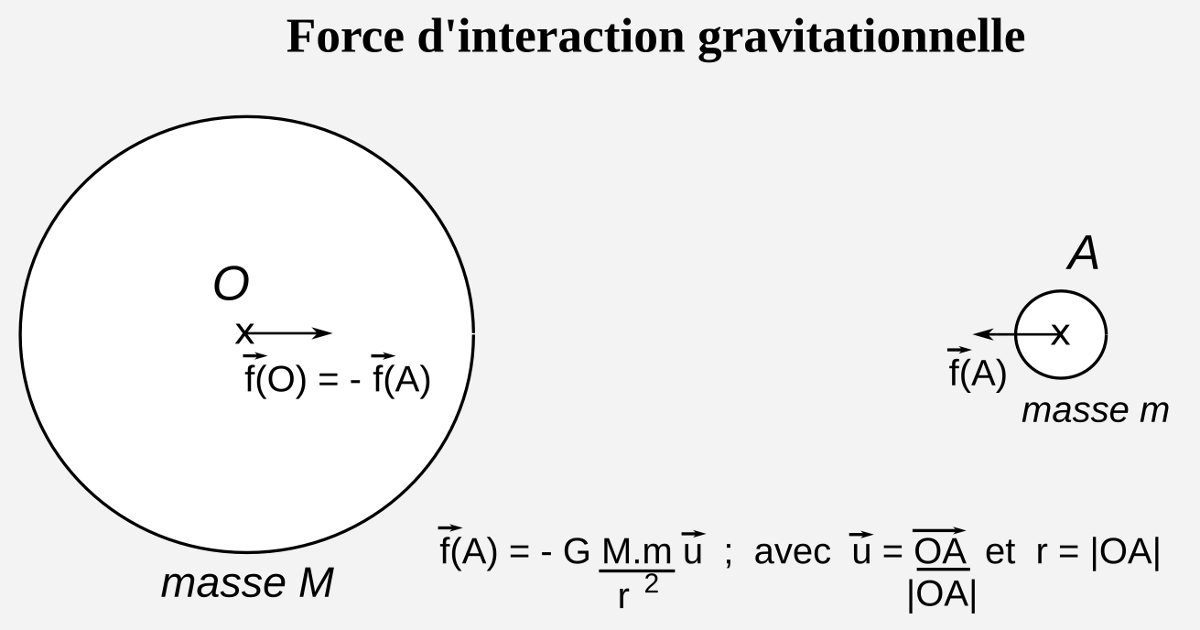
L'expression vectorielle de la force d'interaction gravitationnelle constitue une pierre angulaire de la physique newtonienne. Elle formalise la manière dont deux corps massifs s'attirent mutuellement dans l'espace. Son étude rigoureuse ouvre la voie à la compréhension des phénomènes célestes et terrestres.

La force gravitationnelle est intrinsèquement attractive. Elle s'exerce le long de la ligne joignant les centres de masse des deux corps en interaction. Sa direction est donc fondamentale pour sa définition vectorielle complète.

Mathématiquement, l'expression de la force gravitationnelle exercée par un corps de masse m₁ sur un corps de masse m₂, séparés par une distance r, s'écrit :

F₁₂ = -G (m₁m₂ / r²) u₁₂

où :

F₁₂ est le vecteur force exercée par le corps 1 sur le corps 2. Il s'agit de la force d'attraction que m₁ exerce sur m₂.
G est la constante gravitationnelle universelle. Sa valeur est déterminée expérimentalement et est d'environ 6.674 × 10⁻¹¹ N(m/kg)². Elle quantifie l'intensité de la force gravitationnelle.
m₁ et m₂ sont les masses des deux corps en interaction. Exprimées en kilogrammes (kg), elles déterminent l'amplitude de la force.
r est la distance séparant les centres de masse des deux corps. Exprimée en mètres (m), elle influe inversement sur la force, qui diminue avec le carré de la distance.
u₁₂ est le vecteur unitaire pointant du corps 1 vers le corps 2. Il définit la direction de la force. Son amplitude est égale à 1, il n'a pas d'unité et sert uniquement à orienter la force.
Le signe négatif indique que la force est attractive. Le corps 2 est attiré vers le corps 1.

L'expression ci-dessus est valable pour des corps considérés comme ponctuels ou à symétrie sphérique. Dans le cas de corps de forme irrégulière, il est nécessaire de considérer la distribution de masse et d'intégrer les forces gravitationnelles sur l'ensemble du volume.

H2: Implications et Applications

L'expression vectorielle de la force gravitationnelle a des implications profondes. Elle permet, entre autres :

La prédiction précise des mouvements des planètes, des satellites et des comètes. L'astronomie moderne repose sur ce formalisme.
La détermination de la trajectoire des objets lancés dans le champ gravitationnel terrestre. La balistique et l'astronautique en dépendent.
La compréhension des marées, résultant de l'attraction gravitationnelle de la Lune et du Soleil sur les océans.
L'étude de la formation et de l'évolution des galaxies. La gravité est la force dominante à l'échelle cosmique.

Il est crucial de comprendre que cette expression est une approximation. La relativité générale d'Einstein offre une description plus précise de la gravitation, notamment dans des champs gravitationnels intenses ou à des vitesses proches de celle de la lumière. Cependant, dans la plupart des situations courantes, l'expression newtonienne reste d'une précision remarquable.

La force exercée par le corps 2 sur le corps 1 est simplement l'opposé de la force exercée par le corps 1 sur le corps 2. Ceci est une conséquence directe de la troisième loi de Newton (principe des actions réciproques) :

F₂₁ = - F₁₂ = G (m₁m₂ / r²) u₂₁

où u₂₁ est le vecteur unitaire pointant du corps 2 vers le corps 1. On a clairement u₂₁ = - u₁₂.

L'expression vectorielle de la force gravitationnelle est donc cohérente avec les lois fondamentales de la mécanique.

H2: Considérations Pratiques

Dans les calculs, il est essentiel de respecter les unités du Système International (SI). Les masses doivent être exprimées en kilogrammes (kg), les distances en mètres (m) et la force en newtons (N).

Le choix d'un système de coordonnées approprié peut simplifier considérablement les calculs. Dans de nombreux cas, un système de coordonnées cartésiennes ou sphériques est utilisé.

Lors de la résolution de problèmes impliquant plusieurs corps, il est nécessaire de calculer la force gravitationnelle exercée par chaque corps sur le corps considéré et de sommer vectoriellement ces forces. C'est le principe de superposition.

Il est important de noter que l'expression de la force gravitationnelle ne prend pas en compte d'autres forces qui pourraient agir sur les corps, telles que les forces de frottement ou les forces électromagnétiques.

En conclusion, l'expression vectorielle de la force d'interaction gravitationnelle est un outil puissant pour l'analyse des phénomènes gravitationnels. Sa maîtrise est essentielle pour toute personne étudiant la physique ou l'ingénierie. Elle permet une description quantitative précise de l'attraction entre les masses et ouvre la voie à une compréhension plus profonde de l'univers.