Exercices Droites Parallèles Et Perpendiculaires 6ème Correction

Bienvenue dans le monde rigoureux et fascinant des droites parallèles et perpendiculaires, un pilier fondamental de la géométrie en classe de sixième. Cet article se veut une ressource exhaustive pour maîtriser ces concepts essentiels. Nous explorerons les exercices classiques et leurs corrections détaillées.

L'objectif est de solidifier votre compréhension et de vous fournir les outils nécessaires pour exceller dans vos évaluations.

Définitions et Propriétés Essentielles

Rappelons d'abord les définitions cruciales. Deux droites sont dites parallèles si elles ne se coupent jamais, quelle que soit leur extension. Elles conservent toujours la même distance entre elles.

Deux droites sont perpendiculaires si elles se coupent en formant un angle droit (90 degrés). L'équerre est l'instrument par excellence pour vérifier cette perpendicularité.

La notation est également importante. Pour indiquer que les droites (d1) et (d2) sont parallèles, on écrit (d1) // (d2). Pour la perpendicularité, on utilise le symbole ⊥ : (d1) ⊥ (d2).

Exercices Typiques et Leurs Solutions Détaillées

L'identification des droites parallèles et perpendiculaires est une compétence de base. Des exercices fréquents consistent à observer des figures géométriques et à déterminer quelles droites respectent ces relations.

Exemple 1: Sur une figure complexe comprenant plusieurs droites, identifier toutes les paires de droites parallèles et perpendiculaires. La correction exige une justification précise pour chaque paire identifiée, mentionnant les angles droits ou l'absence d'intersection.

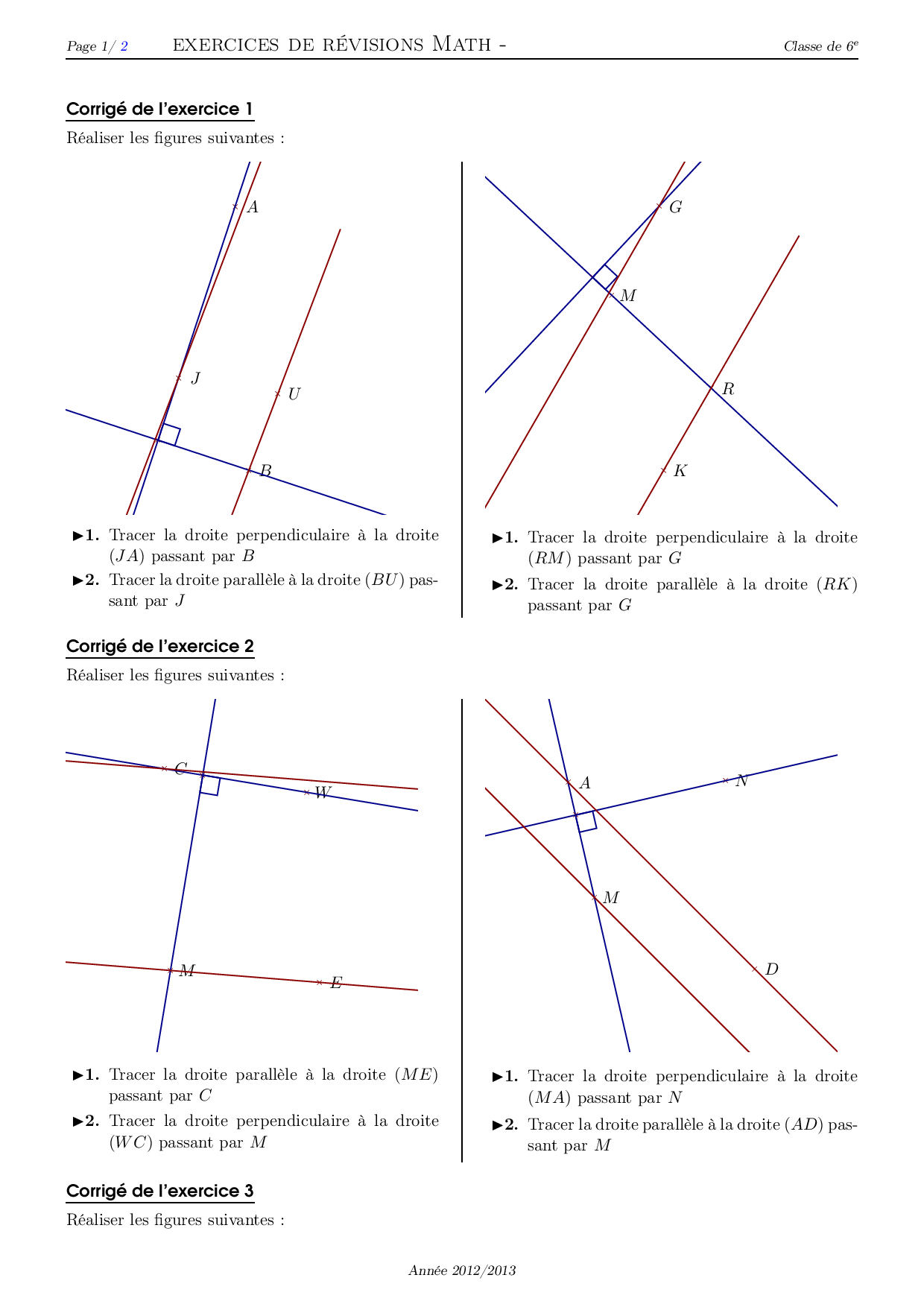
Exemple 2: Tracer une droite (d) puis construire une droite (d') parallèle à (d) passant par un point A donné, extérieur à (d). La solution implique l'utilisation d'une équerre et d'une règle, en veillant à maintenir un angle constant entre les droites. Il est impératif de décrire clairement les étapes de la construction.

Exemple 3: Tracer une droite (d) puis construire une droite (d'') perpendiculaire à (d) passant par un point B donné. Cette construction, similaire à la précédente, requiert une maîtrise de l'équerre pour garantir un angle droit parfait.

Exercices de Construction et de Démonstration

Ces exercices mettent l'accent sur la précision et la rigueur. Ils nécessitent une compréhension approfondie des propriétés.

Exemple 4: Étant donné un quadrilatère ABCD, démontrer que les côtés opposés AB et CD sont parallèles, sachant que les angles ∠ABC et ∠BCD sont supplémentaires. La correction s'appuie sur le théorème des angles alternes-internes.

Exemple 5: Démontrer que si deux droites sont perpendiculaires à une même troisième droite, alors elles sont parallèles entre elles. Cette démonstration utilise le concept d'angles correspondants égaux.

L'Importance de la Précision du Vocabulaire

L'utilisation d'un vocabulaire précis est cruciale. Distinguer clairement les termes "parallèle" et "perpendiculaire" est essentiel. Employer des termes comme "sécantes" (droites qui se coupent) et "coplanaires" (droites situées dans le même plan) enrichit votre compréhension.

Erreurs Fréquentes à Éviter

Plusieurs erreurs reviennent souvent. L'estimation visuelle, sans l'utilisation d'instruments de mesure, peut conduire à des conclusions erronées. Négliger de justifier les constructions et les identifications est également une erreur courante.

Confondre les angles droits avec des angles aigus ou obtus est une autre source d'erreurs. Enfin, une mauvaise manipulation de l'équerre et de la règle compromet la précision des constructions.

Conseils pour une Maîtrise Parfaite

La pratique régulière est le pilier de la réussite. Répéter les exercices et varier les types de problèmes renforce votre compréhension.

Visualiser les concepts dans des situations concrètes, comme les rues parallèles ou les murs perpendiculaires d'une maison, aide à ancrer les connaissances.

Demander de l'aide à votre professeur ou à vos camarades en cas de difficultés est une démarche constructive.

N'hésitez pas à consulter des ressources complémentaires, comme des manuels scolaires ou des sites web éducatifs.

La maîtrise des droites parallèles et perpendiculaires est un tremplin vers des concepts géométriques plus avancés. Une solide base vous sera indispensable pour aborder sereinement les chapitres suivants. La géométrie, bien que rigoureuse, est aussi une source d'émerveillement. En persévérant, vous découvrirez la beauté et la logique qui la sous-tendent.