L'étude de la parité, de l'imparité et de la périodicité d'une fonction est une étape fondamentale dans l'analyse mathématique. Exo7 propose des ressources précieuses pour maîtriser ces concepts. Examinons en détail comment aborder ces notions.
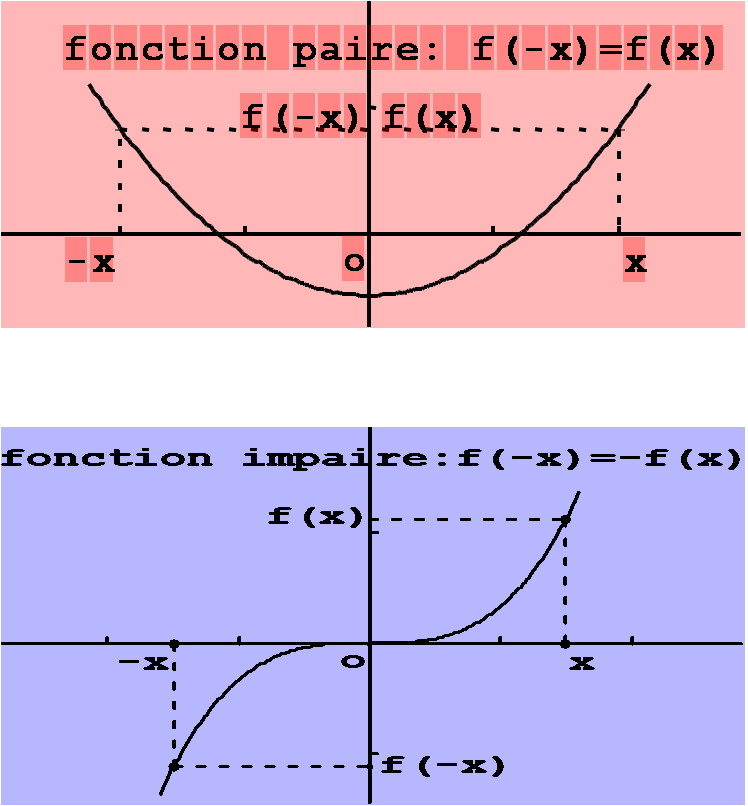
Une fonction paire est caractérisée par sa symétrie par rapport à l'axe des ordonnées. Mathématiquement, cela se traduit par la relation f(-x) = f(x) pour tout x appartenant au domaine de définition de la fonction. Identifier une fonction paire revient donc à vérifier cette égalité. Si elle est vérifiée, la fonction est paire.
À l'inverse, une fonction impaire présente une symétrie par rapport à l'origine du repère. La condition mathématique qui définit une fonction impaire est f(-x) = -f(x) pour tout x dans son domaine. De même, pour prouver qu'une fonction est impaire, il faut démontrer cette égalité.
Il est crucial de noter qu'une fonction n'est pas nécessairement paire ou impaire. Elle peut ne vérifier aucune des deux conditions. Elle est alors qualifiée de fonction ni paire, ni impaire. L'étude de la parité commence donc par l'établissement du domaine de définition. Si le domaine n'est pas symétrique par rapport à zéro, la fonction ne peut être ni paire ni impaire.
Pour déterminer si une fonction est paire ou impaire, on calcule f(-x) et on le compare à f(x) et à -f(x). Ce calcul est la pierre angulaire de l'analyse de parité.
Par exemple, considérons la fonction f(x) = x². Calculons f(-x) : f(-x) = (-x)² = x². On observe que f(-x) = f(x). Par conséquent, la fonction f(x) = x² est paire.
Prenons maintenant la fonction g(x) = x³. Calculons g(-x) : g(-x) = (-x)³ = -x³. On constate que g(-x) = -g(x). Donc, la fonction g(x) = x³ est impaire.
Périodicité
La périodicité est une autre propriété importante des fonctions. Une fonction est dite périodique s'il existe un nombre réel T non nul, appelé période, tel que f(x + T) = f(x) pour tout x dans le domaine de définition. La période T représente l'intervalle après lequel la fonction se répète identiquement.
La détermination de la période, si elle existe, est essentielle. Pour ce faire, on cherche à identifier une valeur T qui satisfait la condition de périodicité. Dans certains cas, la période peut être directement observable à partir de l'expression de la fonction. Dans d'autres, des manipulations algébriques sont nécessaires.
Considérons la fonction trigonométrique f(x) = sin(x). Nous savons que sin(x + 2π) = sin(x) pour tout x. Ainsi, la fonction sinus est périodique de période 2π.
De manière générale, les fonctions trigonométriques telles que sinus et cosinus sont périodiques. Leur période est 2π. La fonction tangente est également périodique, mais sa période est π.
Pour démontrer qu'une fonction est périodique, il faut identifier la période T et vérifier que f(x + T) = f(x) pour tout x dans le domaine.
L'étude de la parité et de la périodicité permet de simplifier l'étude des fonctions. La connaissance de ces propriétés réduit le domaine d'étude et facilite le tracé de la courbe représentative. Par exemple, si une fonction est paire, il suffit de l'étudier sur les réels positifs et de compléter la courbe par symétrie par rapport à l'axe des ordonnées. Si elle est impaire, on utilise une symétrie par rapport à l'origine.
De même, si une fonction est périodique, on peut se contenter de l'étudier sur un intervalle de longueur égale à la période. La courbe se répète ensuite à l'infini.
En conclusion, la maîtrise des concepts de parité, d'imparité et de périodicité est indispensable pour l'analyse des fonctions. Exo7 offre des exercices et des ressources pédagogiques pour approfondir ces notions et acquérir une solide compréhension. Une pratique régulière est essentielle pour maîtriser ces concepts et les appliquer avec succès.
étude de la représentation graphique d'une fonction