Comment Montrer Qu'une Droite Est Orthogonale A Un Plan

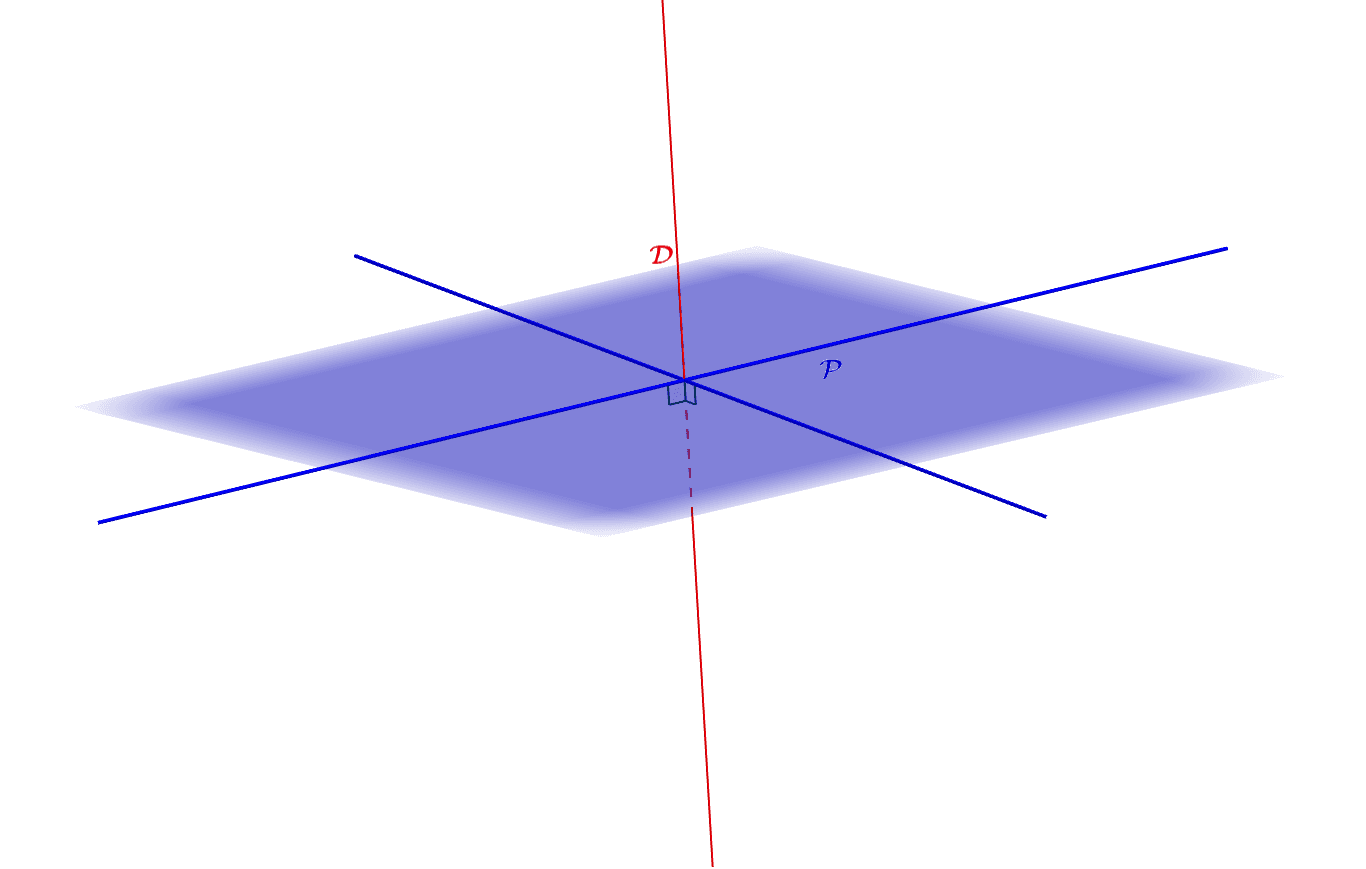
Montrer qu'une droite est orthogonale à un plan est une compétence fondamentale en géométrie de l'espace. Voici les méthodes rigoureuses pour y parvenir.

Pour démontrer l'orthogonalité d'une droite par rapport à un plan, il faut prouver qu'elle est orthogonale à deux droites sécantes contenues dans ce plan. C'est le théorème fondamental que nous allons exploiter.

Considérez une droite (d) et un plan (P). Notre objectif est de prouver que (d) est perpendiculaire à (P).

Commencez par identifier deux droites distinctes, (d1) et (d2), situées intégralement dans le plan (P). Assurez-vous que ces deux droites se coupent en un point précis. Nommons ce point d'intersection A.

Ensuite, démontrez rigoureusement que la droite (d) est perpendiculaire à la droite (d1). Pour cela, calculez le produit scalaire des vecteurs directeurs de (d) et (d1). Si ce produit scalaire est nul, alors (d) et (d1) sont orthogonales.

Répétez l'étape précédente pour la droite (d2). Calculez le produit scalaire des vecteurs directeurs de (d) et (d2). Si ce produit scalaire est nul, alors (d) et (d2) sont orthogonales.

Si vous avez démontré que (d) est perpendiculaire à (d1) et (d2), et que (d1) et (d2) sont sécantes dans (P), alors vous pouvez conclure avec certitude que (d) est orthogonale au plan (P).

Utilisation du vecteur normal

Une autre approche consiste à utiliser le vecteur normal d'un plan. Chaque plan possède un vecteur normal, qui est un vecteur perpendiculaire à tout vecteur contenu dans le plan.

Déterminez une équation cartésienne du plan (P). Cette équation sera de la forme ax + by + cz + d = 0, où a, b, c et d sont des constantes.

Identifiez le vecteur normal du plan (P). Ce vecteur est donné par ses composantes : n = (a, b, c).

Déterminez un vecteur directeur de la droite (d). Appelons ce vecteur u.

Vérifiez si les vecteurs n et u sont colinéaires. Pour cela, il faut vérifier si les composantes de n sont proportionnelles aux composantes de u. Autrement dit, il doit exister un scalaire k tel que n = k * u.

Si vous constatez que n et u sont colinéaires, alors vous pouvez conclure que la droite (d) est orthogonale au plan (P). La colinéarité des vecteurs normal et directeur implique la perpendicularité entre la droite et le plan.

Cas particulier : droite définie par deux points

Si la droite (d) est définie par deux points A et B, vous pouvez déterminer son vecteur directeur en calculant le vecteur AB = B - A.

Ensuite, vous suivez les étapes décrites précédemment, en utilisant le vecteur AB comme vecteur directeur de la droite (d).

Exemple concret

Supposons que le plan (P) soit défini par l'équation x + 2y - z + 3 = 0, et que la droite (d) ait pour vecteur directeur u = (1, 2, -1).

Le vecteur normal du plan (P) est n = (1, 2, -1).

Nous constatons que u = n. Les vecteurs sont donc colinéaires (k = 1).

Nous pouvons donc conclure que la droite (d) est orthogonale au plan (P).

Difficultés et pièges à éviter

Assurez-vous que les droites (d1) et (d2) sont bien sécantes. Si elles sont parallèles, cela ne suffit pas pour prouver l'orthogonalité.

Vérifiez attentivement les calculs des produits scalaires et des vecteurs directeurs. Une erreur de calcul peut invalider toute la démonstration.

N'oubliez pas de mentionner explicitement que les droites (d1) et (d2) sont contenues dans le plan (P).

Soyez précis dans votre rédaction. Utilisez un vocabulaire mathématique rigoureux et évitez les approximations.

En suivant ces étapes avec rigueur et précision, vous serez en mesure de démontrer l'orthogonalité d'une droite par rapport à un plan de manière irréfutable. La clarté de la démonstration est aussi importante que la justesse des calculs.