Comment Calculer Le Volume D'un Cylindre De Révolution

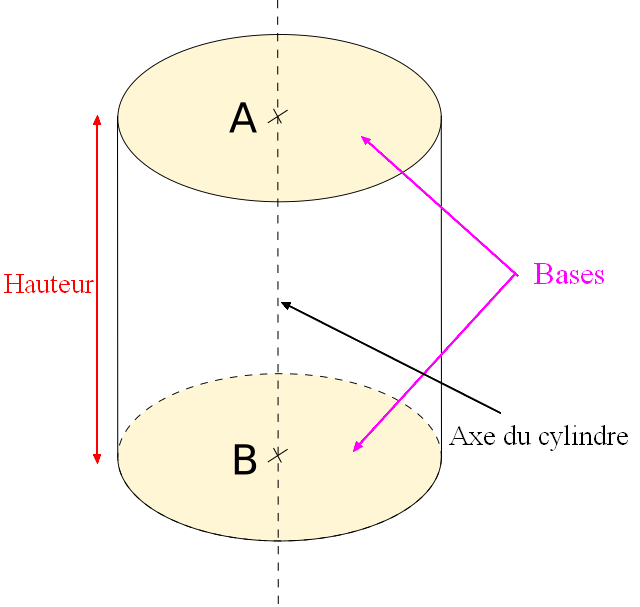
Le calcul du volume d'un cylindre de révolution est une opération fondamentale en géométrie. Voici une explication détaillée de la méthode.

La formule de base est la suivante :

V = πr²h

Où :

V représente le volume du cylindre.
π (pi) est une constante mathématique approximativement égale à 3,14159.
r est le rayon du cercle de base du cylindre.
h est la hauteur du cylindre.

Détermination du Rayon (r)

Le rayon est la distance entre le centre du cercle de base et n'importe quel point de sa circonférence. Si vous connaissez le diamètre (d) du cercle, le rayon est simplement la moitié du diamètre :

r = d / 2

Si vous ne connaissez que la circonférence (C) du cercle de base, vous pouvez calculer le rayon avec la formule :

r = C / (2π)

Mesure de la Hauteur (h)

La hauteur est la distance perpendiculaire entre les deux bases circulaires du cylindre. Assurez-vous que la mesure est prise perpendiculairement à la base.

Calcul de l'Aire de la Base (πr²)

Calculez d'abord le carré du rayon (r²). Ensuite, multipliez le résultat par π (approximativement 3,14159). Ceci vous donne l'aire de la base circulaire.

Calcul du Volume (V)

Multipliez l'aire de la base (πr²) par la hauteur (h) du cylindre. Le résultat est le volume (V) du cylindre.

Unités de Mesure

Assurez-vous que toutes les mesures (rayon et hauteur) sont exprimées dans les mêmes unités. Si le rayon et la hauteur sont en centimètres (cm), le volume sera en centimètres cubes (cm³). Si le rayon et la hauteur sont en mètres (m), le volume sera en mètres cubes (m³).

Exemple de Calcul

Supposons un cylindre avec un rayon de 5 cm et une hauteur de 10 cm.

Aire de la base : πr² = π * (5 cm)² = π * 25 cm² ≈ 78,54 cm²
Volume : V = Aire de la base * hauteur = 78,54 cm² * 10 cm = 785,4 cm³

Le volume du cylindre est donc d'environ 785,4 cm³.

Cas Particuliers et Précisions

Si le cylindre est incliné, la hauteur (h) doit être mesurée perpendiculairement à la base. Il est important d'utiliser une équerre pour garantir la précision de la mesure.

Si le cylindre est creux (un tube), calculez le volume du cylindre extérieur, puis soustrayez le volume du cylindre intérieur. Cela vous donnera le volume du matériau composant le cylindre creux.

V = π(r_externe² - r_interne²)h

Où :

r_externe est le rayon extérieur du cylindre.
r_interne est le rayon intérieur du cylindre.

Utilisation d'Outils de Calcul

De nombreux calculateurs en ligne peuvent effectuer ce calcul automatiquement. Entrez simplement les valeurs du rayon et de la hauteur. Ces outils minimisent les erreurs d'arrondi.

Approfondissement des Notions

La formule du volume d'un cylindre est une application directe du principe général du volume d'un prisme : aire de la base multipliée par la hauteur. Le cercle étant une forme géométrique bien définie, le calcul de son aire (et donc du volume du cylindre) est relativement simple.

Importance de la Précision

La précision des mesures du rayon et de la hauteur est cruciale pour obtenir un volume précis. Des erreurs minimes dans les mesures peuvent entraîner des erreurs significatives dans le calcul du volume. Utilisez des instruments de mesure précis, tels qu'un pied à coulisse, pour minimiser ces erreurs.

Applications Pratiques

Le calcul du volume d'un cylindre est essentiel dans de nombreux domaines :

Ingénierie: Conception de réservoirs, de tuyaux, et d'autres structures cylindriques.
Construction: Estimation des matériaux nécessaires pour des piliers cylindriques ou des fondations.
Chimie: Calcul du volume de réacteurs cylindriques.
Physique: Détermination de la capacité de récipients cylindriques.
Fabrication: Production de pièces cylindriques avec des dimensions précises.

Conseils Utiles

Vérifiez toujours les unités de mesure avant de commencer le calcul. Convertissez si nécessaire.
Utilisez une calculatrice avec une fonction π pour une plus grande précision.
Si vous effectuez des calculs manuels, utilisez au moins cinq décimales pour π (3.14159) pour minimiser les erreurs d'arrondi.
Pour les cylindres creux, assurez-vous de mesurer précisément les rayons intérieur et extérieur.

Conclusion

Le calcul du volume d'un cylindre de révolution est une opération simple et directe. En comprenant la formule et en suivant les étapes décrites, vous pouvez calculer avec précision le volume de n'importe quel cylindre. N'oubliez pas l'importance de la précision des mesures et de l'utilisation des unités appropriées.