Comment Calculer L'aire De La Base D'un Prisme Droit

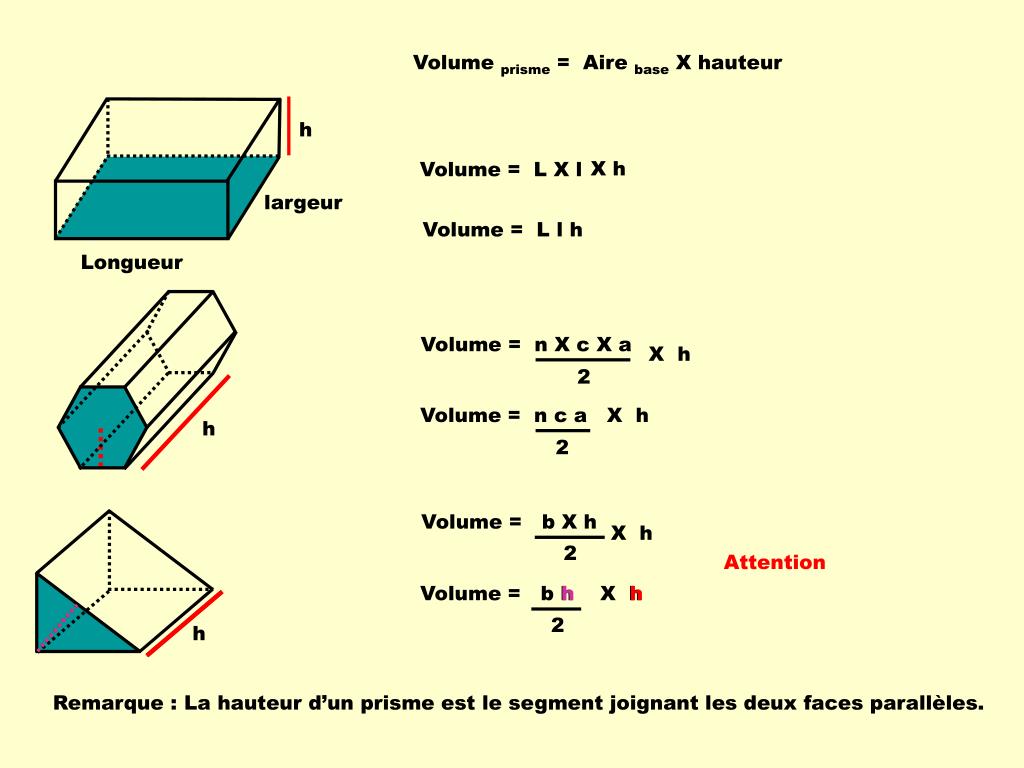
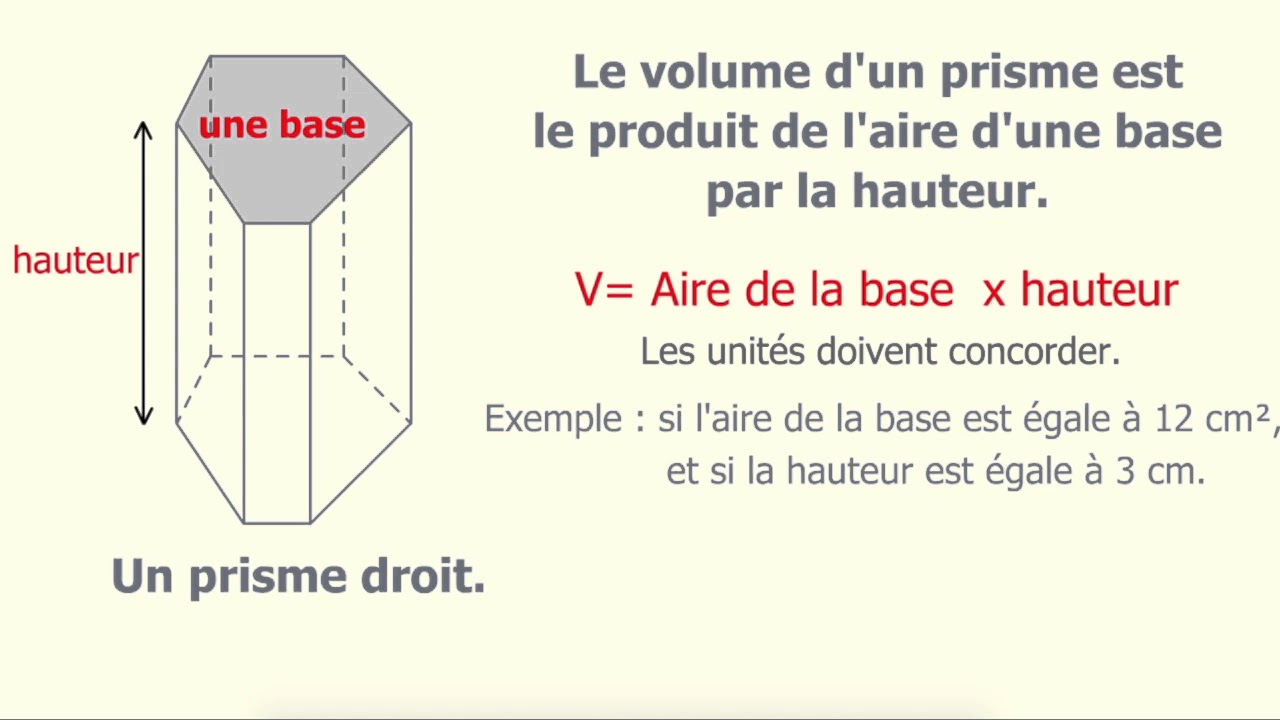
Calculer l'aire de la base d'un prisme droit est fondamental pour déterminer son volume et son aire totale. La méthode précise dépend de la forme de cette base. Examinons les différents cas de figure.

Commençons par le triangle. La base triangulaire requiert la formule classique : (base * hauteur) / 2. Identifiez la base et la hauteur correspondante du triangle. Multipliez ces deux valeurs. Divisez ensuite le résultat par deux. Vous obtiendrez l'aire de la base triangulaire.

Si la base est un carré ou un rectangle, le calcul est simplifié. Pour un carré, l'aire est simplement le côté multiplié par lui-même (côté²). Pour un rectangle, multipliez la longueur par la largeur. Ces calculs directs fournissent l'aire de la base quadrilatérale.

La base peut également être un cercle. Dans ce cas, utilisez la formule πr², où r représente le rayon du cercle. Mesurez le rayon. Élevez-le au carré. Multipliez le résultat par π (environ 3,14159). Vous obtiendrez l'aire de la base circulaire.

Si la base est un trapèze, l'aire se calcule par la formule suivante : ((petite base + grande base) * hauteur) / 2. Additionnez les longueurs des deux bases parallèles. Multipliez cette somme par la hauteur du trapèze. Divisez le résultat par deux. L'aire de la base trapézoïdale est ainsi déterminée.

Une base polygonale régulière nécessite une approche différente. Utilisez la formule (périmètre * apothème) / 2. Le périmètre est la somme des longueurs de tous les côtés. L'apothème est la distance du centre du polygone au milieu d'un côté. Multipliez le périmètre par l'apothème. Divisez ensuite le résultat par deux.

Dans le cas d'un polygone irrégulier, divisez-le en formes plus simples. Triangles, rectangles et trapèzes sont les plus courants. Calculez l'aire de chaque forme. Additionnez toutes ces aires. Vous obtiendrez l'aire totale du polygone irrégulier.

Exemples pratiques :

Prenons un prisme droit à base triangulaire. Supposons que la base du triangle mesure 6 cm et sa hauteur 4 cm. L'aire de la base est (6 cm * 4 cm) / 2 = 12 cm².

Considérons un prisme droit à base rectangulaire. La longueur du rectangle est de 8 cm et sa largeur de 5 cm. L'aire de la base est 8 cm * 5 cm = 40 cm².

Pour un prisme droit à base circulaire avec un rayon de 3 cm. L'aire de la base est π * (3 cm)² ≈ 28,27 cm².

Imaginez un prisme droit à base trapézoïdale. La petite base mesure 4 cm, la grande base 8 cm et la hauteur 3 cm. L'aire de la base est ((4 cm + 8 cm) * 3 cm) / 2 = 18 cm².

Un prisme droit à base hexagonale régulière avec un côté de 5 cm et un apothème de 4,33 cm. Le périmètre est 6 * 5 cm = 30 cm. L'aire de la base est (30 cm * 4,33 cm) / 2 ≈ 64,95 cm².

Importance de l'unité de mesure :

N'oubliez jamais d'indiquer l'unité de mesure de l'aire. Elle sera toujours exprimée au carré (cm², m², etc.). Une unité incorrecte rendra votre calcul inutilisable.

Vérification :

Après chaque calcul, vérifiez vos résultats. Assurez-vous que les valeurs utilisées sont correctes. Examinez le résultat pour détecter d'éventuelles erreurs grossières. Un résultat absurde indique une faute de calcul.

Outils :

Utilisez une calculatrice pour effectuer les opérations. Géogébra et d'autres logiciels de géométrie peuvent vous aider à visualiser les formes et à vérifier vos calculs.

Cas complexes :

Parfois, la base du prisme peut être une combinaison de formes. Dans ce cas, divisez la base en sections plus simples. Calculez l'aire de chaque section. Additionnez ces aires pour obtenir l'aire totale de la base. Cette approche est particulièrement utile pour les formes irrégulières. Elle permet de simplifier le problème en le décomposant en éléments plus facilement gérables.

Enfin, la précision des mesures initiales est cruciale. Une mesure imprécise affectera l'exactitude du résultat final. Utilisez des instruments de mesure appropriés et effectuez plusieurs mesures pour minimiser les erreurs. L'attention aux détails est essentielle pour obtenir un résultat fiable et précis.