Comment Calculer La Mesure D'un Angle Dans Un Triangle Rectangle

$Comment Calculer La Mesure D'un Angle Dans Un Triangle Rectangle Comment Calculer La Mesure D Un Angle Dans Un Triangl - vrogue.co$

Dans le domaine fascinant de la géométrie, le triangle rectangle occupe une place de choix. Sa particularité, un angle droit, en fait un outil précieux pour de nombreux calculs. Déterminer la mesure d'un angle aigu dans un triangle rectangle est une compétence fondamentale. Nous allons explorer les méthodes à votre disposition.

Pour aborder ce calcul, plusieurs approches se présentent. Le choix de la méthode dépend des informations dont vous disposez initialement.

Utilisation des Fonctions Trigonométriques

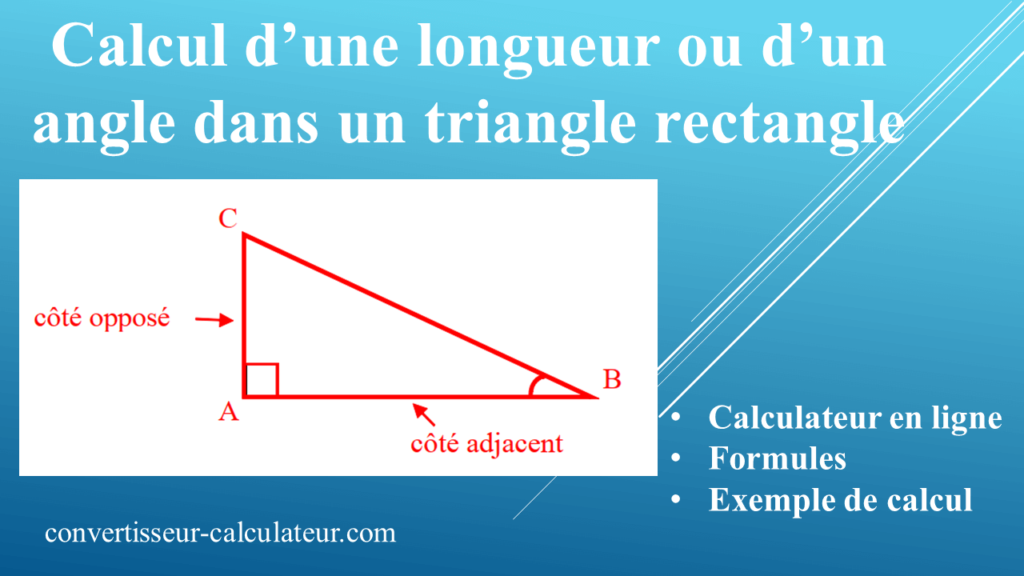
C’est l'approche la plus courante. Les fonctions trigonométriques, sinus (sin), cosinus (cos) et tangente (tan), établissent des relations entre les angles aigus et les côtés du triangle rectangle.

Sinus (sin): Le sinus d'un angle aigu est le rapport entre la longueur du côté opposé à cet angle et la longueur de l'hypoténuse. sin(angle) = Côté Opposé / Hypoténuse
Cosinus (cos): Le cosinus d'un angle aigu est le rapport entre la longueur du côté adjacent à cet angle et la longueur de l'hypoténuse. cos(angle) = Côté Adjacent / Hypoténuse
Tangente (tan): La tangente d'un angle aigu est le rapport entre la longueur du côté opposé à cet angle et la longueur du côté adjacent à cet angle. tan(angle) = Côté Opposé / Côté Adjacent

Pour déterminer la mesure d'un angle, vous devez d'abord identifier le rapport trigonométrique approprié en fonction des côtés connus. Ensuite, utilisez la fonction trigonométrique inverse correspondante (arcsin, arccos ou arctan) sur votre calculatrice.

Par exemple, si vous connaissez la longueur du côté opposé et de l'hypoténuse, calculez le sinus de l'angle. Puis, appliquez la fonction arcsin (sin⁻¹) à ce résultat pour obtenir la mesure de l'angle en degrés.

Théorème de Pythagore et Somme des Angles

Le théorème de Pythagore est utile pour déterminer la longueur d'un côté si vous connaissez les deux autres. Rappelez-vous : dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés (a² + b² = c²).

Si vous connaissez la longueur de deux côtés, utilisez le théorème de Pythagore pour trouver le troisième. Vous pourrez ensuite utiliser les fonctions trigonométriques décrites précédemment.

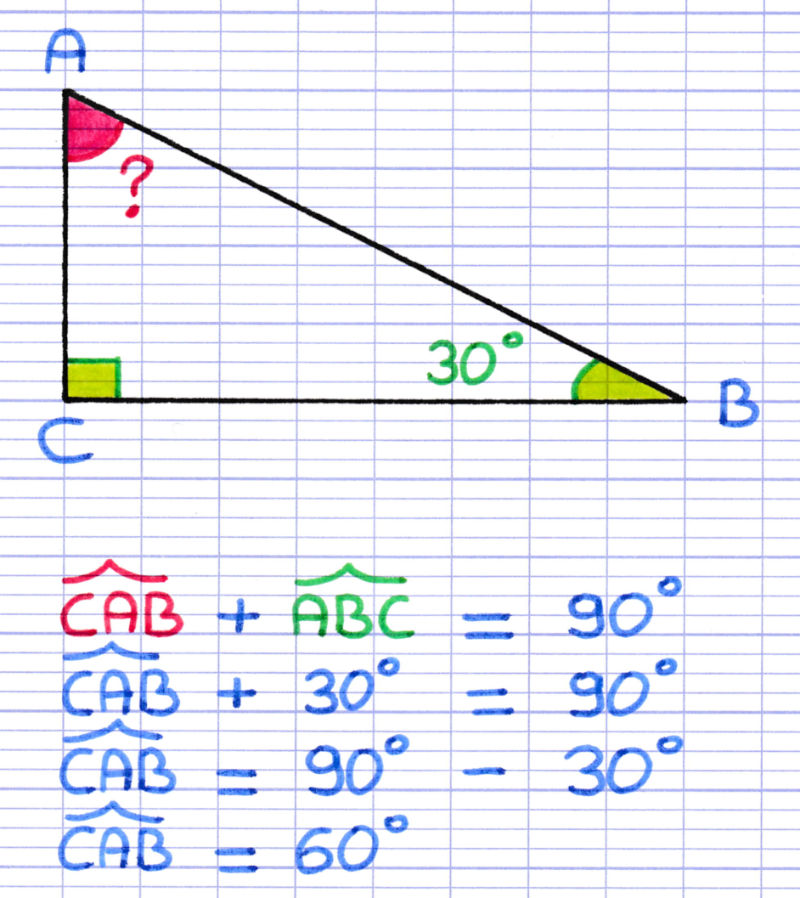
La somme des angles d'un triangle est toujours égale à 180 degrés. Dans un triangle rectangle, l'un des angles est de 90 degrés. Par conséquent, la somme des deux autres angles aigus est de 90 degrés. Si vous connaissez la mesure d'un angle aigu, soustrayez-la de 90 degrés pour trouver la mesure de l'autre angle aigu.

Exemple Pratique

Considérons un triangle rectangle ABC, où l'angle en B est droit (90 degrés). Supposons que le côté AB (adjacent à l'angle A) mesure 5 cm et que le côté BC (opposé à l'angle A) mesure 7 cm.

Pour trouver la mesure de l'angle A, utilisez la tangente. tan(A) = BC / AB = 7 / 5 = 1.4

Appliquez la fonction arctan (tan⁻¹) à 1.4 pour obtenir la mesure de l'angle A. A = arctan(1.4) ≈ 54.46 degrés

L'angle C peut être trouvé en soustrayant l'angle A de 90 degrés. C = 90 - 54.46 ≈ 35.54 degrés.

Précautions et Erreurs Courantes

Assurez-vous que votre calculatrice est réglée sur le mode approprié (degrés ou radians). L'utilisation d'une unité incorrecte conduira à des résultats erronés. Vérifiez attentivement quelles sont les mesures de côtés donnés, adjacent, opposé ou hypoténuse, pour ne pas vous tromper dans le choix de la fonction trigonométrique.

Il est crucial de bien identifier les côtés du triangle rectangle par rapport à l'angle que vous cherchez à calculer. Une mauvaise identification conduira à l'utilisation d'un rapport trigonométrique incorrect et donc à un résultat erroné.

Conclusion

Calculer la mesure d'un angle dans un triangle rectangle est un processus précis. Les fonctions trigonométriques et le théorème de Pythagore sont des outils puissants. La rigueur et la méthode sont vos meilleurs alliés pour résoudre ces problèmes.