Comment Calculer La Hauteur D'une Pyramide à Base Rectangulaire

Calculer la hauteur d'une pyramide à base rectangulaire requiert la connaissance de certaines dimensions clés. Plusieurs méthodes existent. Chacune dépend des informations dont vous disposez initialement.

Méthode 1 : Connaissant le Volume et les Dimensions de la Base

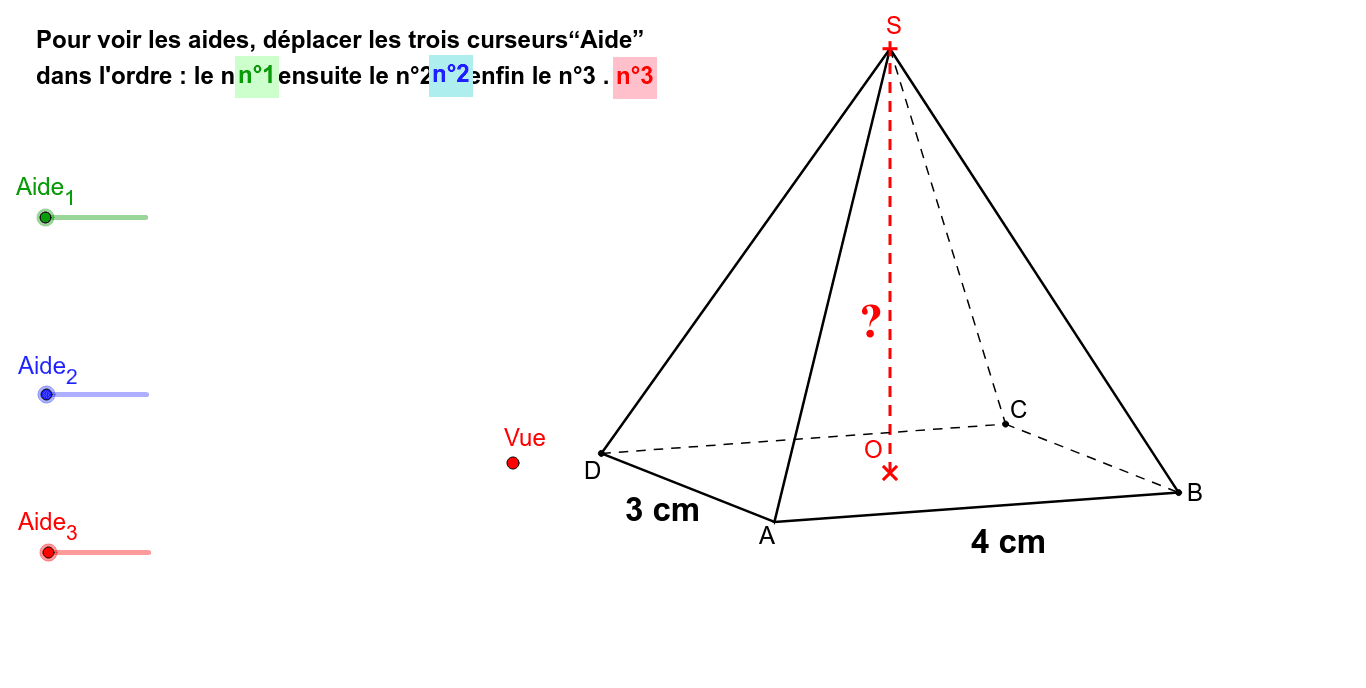
Si vous connaissez le volume (V), la longueur (L) et la largeur (l) de la base rectangulaire, le calcul de la hauteur (h) est direct. La formule du volume d'une pyramide est V = (1/3) * L * l * h.

Pour isoler h, on réarrange la formule : h = (3 * V) / (L * l).

Divisez trois fois le volume par le produit de la longueur et de la largeur de la base. Le résultat est la hauteur.

Méthode 2 : Connaissant l'Apothème et un Côté de la Base

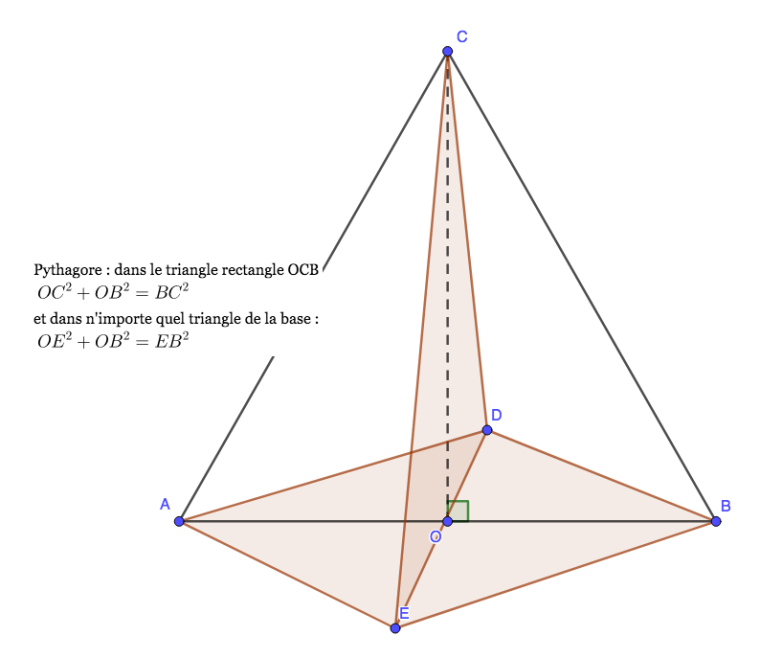
L'apothème est la distance entre le sommet de la pyramide et le milieu d'un côté de la base. Si vous connaissez l'apothème (a) relative à un côté de la base et la longueur (L) ou la largeur (l) de ce côté, vous pouvez utiliser le théorème de Pythagore.

Considérez un triangle rectangle formé par :

La hauteur de la pyramide (h).
La moitié de la longueur (L/2) ou de la largeur (l/2) de la base.
L'apothème (a) correspondant au côté utilisé.

Alors, a² = h² + (L/2)² ou a² = h² + (l/2)².

Isolez h² : h² = a² - (L/2)² ou h² = a² - (l/2)².

Calculez la racine carrée de h² pour obtenir la hauteur : h = √(a² - (L/2)²) ou h = √(a² - (l/2)²).

Méthode 3 : Connaissant l'Arête Latérale et la Moitié des Dimensions de la Base

L'arête latérale est la distance entre le sommet de la pyramide et un sommet de la base. Si vous connaissez l'arête latérale (c) et la moitié de la longueur (L/2) et de la largeur (l/2) de la base, vous utiliserez également le théorème de Pythagore, mais en deux étapes.

D'abord, calculez la distance (d) entre le centre de la base et un sommet de la base. Utilisez le théorème de Pythagore : d² = (L/2)² + (l/2)². Donc, d = √((L/2)² + (l/2)²).

Ensuite, considérez le triangle rectangle formé par :

La hauteur (h) de la pyramide.
La distance (d) calculée précédemment.
L'arête latérale (c).

Utilisez le théorème de Pythagore : c² = h² + d².

Isolez h² : h² = c² - d².

Calculez la racine carrée de h² pour obtenir la hauteur : h = √(c² - d²).

Méthode 4 : Connaissant l'Angle au Sommet et les Dimensions de la Base

Si vous connaissez l'angle au sommet (θ) formé par deux arêtes latérales adjacentes et les dimensions de la base (L et l), le calcul est plus complexe. Il faut d'abord déterminer la distance du centre de la base à un sommet de la base (d) comme dans la méthode 3 : d = √((L/2)² + (l/2)²).

Ensuite, considérez le triangle isocèle formé par les deux arêtes latérales et la diagonale de la base reliant les sommets correspondants. La hauteur de ce triangle, issue du sommet de la pyramide, coupe l'angle θ en deux.

Calculez la moitié de l'angle au sommet : θ/2.

Utilisez la trigonométrie. La tangente de θ/2 est égale à la moitié de la diagonale de la base divisée par la hauteur du triangle isocèle (que nous appellerons "m").

Donc, tan(θ/2) = (√(L² + l²) / 2) / m.

Isolez m : m = (√(L² + l²) / 2) / tan(θ/2).

Enfin, utilisez le théorème de Pythagore avec la hauteur de la pyramide (h), la distance du centre de la base à un sommet (d), et la hauteur du triangle isocèle (m) : h² = m² - d².

Calculez la racine carrée de h² : h = √(m² - d²).

Précisions et Erreurs à Éviter

Assurez-vous que toutes les unités de mesure sont cohérentes (par exemple, toutes en centimètres ou en mètres). Si les unités sont différentes, convertissez-les avant de commencer les calculs.

N'oubliez pas que la formule du volume d'une pyramide est (1/3) * aire de la base * hauteur. L'aire de la base rectangulaire est simplement L * l.

Soyez précis dans vos calculs, surtout lors de la prise de racines carrées. Utilisez une calculatrice pour éviter les erreurs d'arrondi.

Lors de l'utilisation du théorème de Pythagore, identifiez correctement l'hypoténuse et les côtés adjacents au bon angle. Une confusion peut conduire à des résultats incorrects.

La méthode avec l'angle au sommet est la plus complexe et la plus susceptible de contenir des erreurs. Vérifiez attentivement vos calculs trigonométriques.

Ces méthodes vous fourniront la hauteur de la pyramide avec précision, à condition que les informations de départ soient exactes. Choisissez la méthode appropriée en fonction des données disponibles.