Classification En Groupes Emboités Collège Exercices

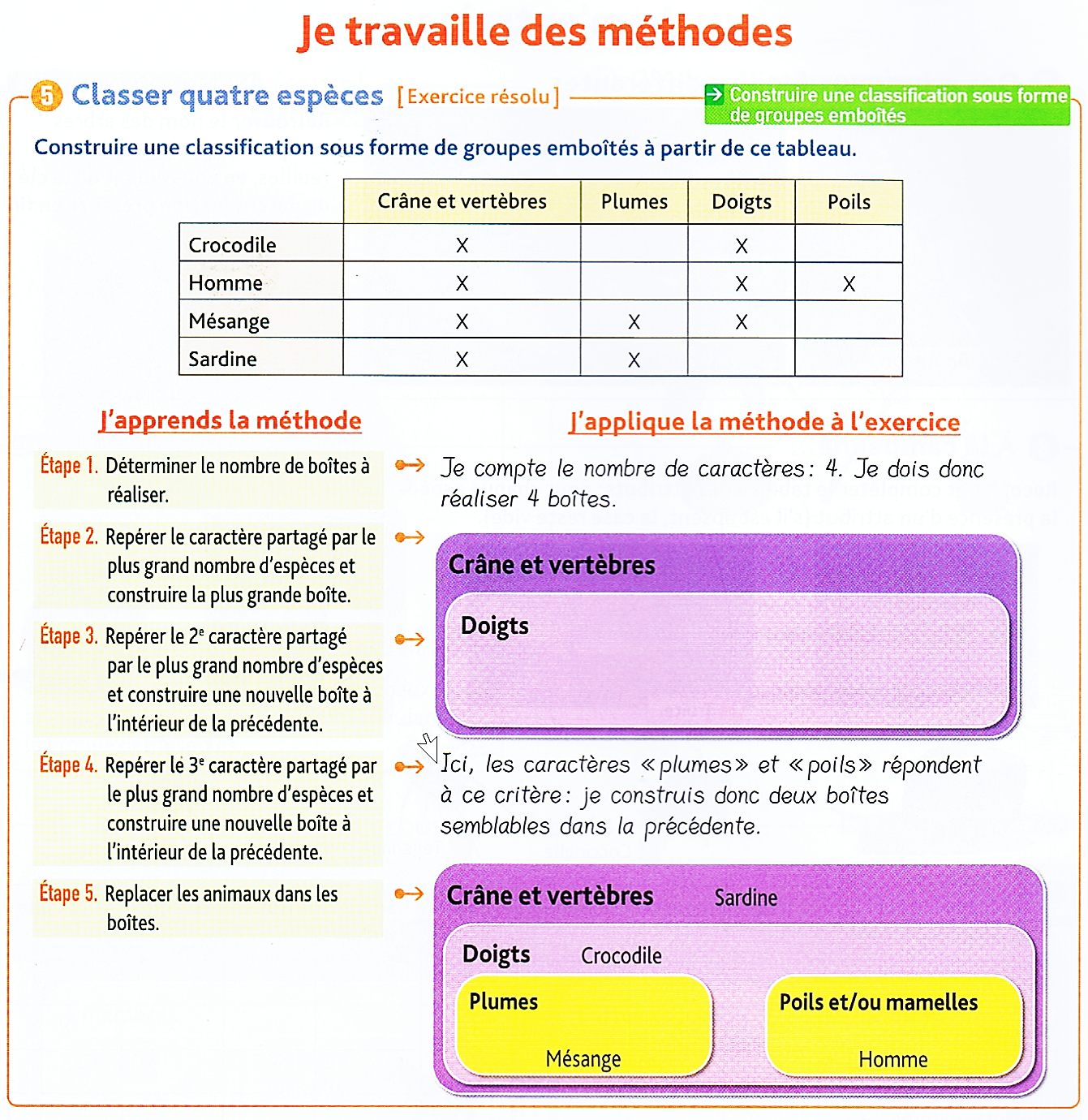
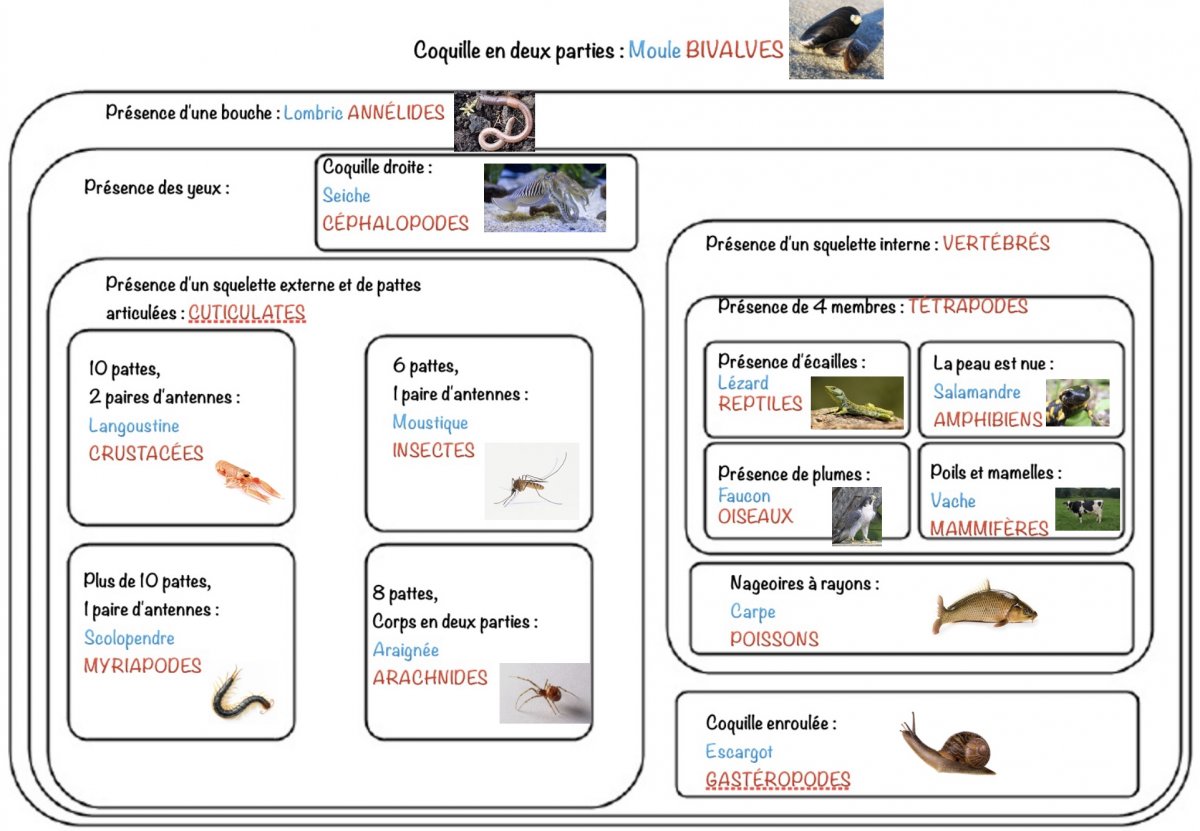
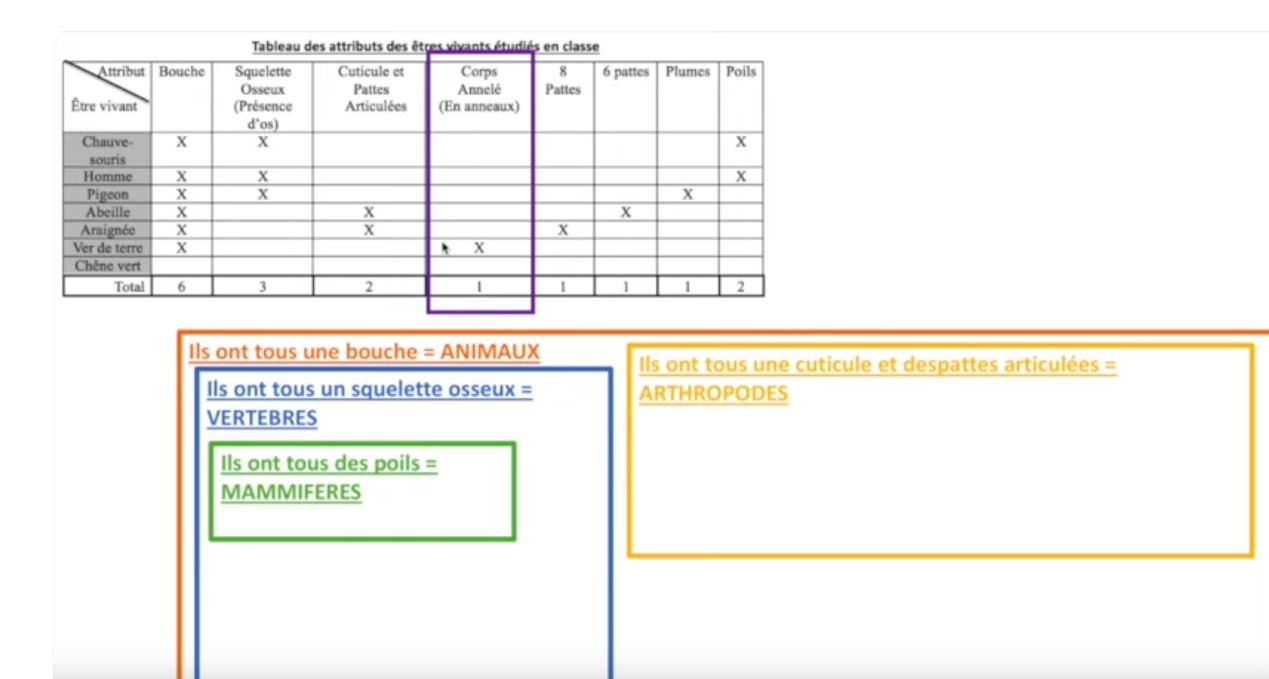
L'étude de la classification en groupes emboîtés au collège est cruciale. Elle forge les bases de la logique ensembliste. Elle prépare aux concepts mathématiques plus avancés. La maîtrise des exercices est essentielle.

Un ensemble est une collection d'objets. Ces objets sont appelés éléments. On utilise souvent des accolades pour délimiter un ensemble. A = {1, 2, 3} est un exemple.

Un ensemble peut être vide. Il ne contient aucun élément. On le note ∅.

Inclusion et appartenance

L'appartenance désigne la relation d'un élément à un ensemble. On utilise le symbole ∈. 1 ∈ A signifie que 1 appartient à A.

L'inclusion désigne la relation d'un ensemble à un autre. On utilise le symbole ⊂. B ⊂ A signifie que B est inclus dans A. Tous les éléments de B sont aussi des éléments de A.

Si A = B, alors A ⊂ B et B ⊂ A.

Si A ⊂ B et A ≠ B, alors A est une partie stricte de B.

Intersection et Réunion

L'intersection de deux ensembles A et B, notée A ∩ B, est l'ensemble des éléments qui appartiennent à A et à B.

La réunion de deux ensembles A et B, notée A ∪ B, est l'ensemble des éléments qui appartiennent à A ou à B (ou aux deux).

Exemples d'exercices et leurs solutions

Soient A = {1, 2, 3, 4, 5}, B = {2, 4, 6, 8} et C = {1, 3, 5, 7, 9}.

Déterminons A ∩ B. Les éléments communs à A et B sont 2 et 4. Donc A ∩ B = {2, 4}.

Déterminons A ∪ B. On combine tous les éléments de A et B sans répétition. Donc A ∪ B = {1, 2, 3, 4, 5, 6, 8}.

Déterminons A ∩ C. Les éléments communs à A et C sont 1, 3 et 5. Donc A ∩ C = {1, 3, 5}.

Déterminons B ∩ C. Il n'y a aucun élément commun à B et C. Donc B ∩ C = ∅.

Déterminons A ∪ C. On combine tous les éléments de A et C sans répétition. Donc A ∪ C = {1, 2, 3, 4, 5, 7, 9}.

Déterminons B ∪ C. On combine tous les éléments de B et C sans répétition. Donc B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8, 9}.

Soit E l'ensemble des nombres pairs compris entre 1 et 10. E = {2, 4, 6, 8, 10}.

Soit F l'ensemble des nombres impairs compris entre 1 et 10. F = {1, 3, 5, 7, 9}.

Soit G l'ensemble des nombres premiers compris entre 1 et 10. G = {2, 3, 5, 7}.

Déterminons E ∩ F. Il n'y a aucun élément commun. Donc E ∩ F = ∅.

Déterminons E ∩ G. Le seul élément commun est 2. Donc E ∩ G = {2}.

Déterminons F ∩ G. Les éléments communs sont 3, 5 et 7. Donc F ∩ G = {3, 5, 7}.

Déterminons E ∪ F. On obtient tous les nombres de 1 à 10. Donc E ∪ F = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Déterminons E ∪ G. E ∪ G = {2, 3, 4, 5, 6, 7, 8, 10}.

Déterminons F ∪ G. F ∪ G = {1, 2, 3, 5, 7, 9}.

Exercices avec conditions

Soit A l'ensemble des multiples de 3 inférieurs à 20. A = {3, 6, 9, 12, 15, 18}.

Soit B l'ensemble des multiples de 5 inférieurs à 20. B = {5, 10, 15}.

Déterminons A ∩ B. Le seul élément commun est 15. Donc A ∩ B = {15}.

Déterminons A ∪ B. A ∪ B = {3, 5, 6, 9, 10, 12, 15, 18}.

Soit C l'ensemble des diviseurs de 12. C = {1, 2, 3, 4, 6, 12}.

Déterminons A ∩ C. Les éléments communs sont 3 et 6. Donc A ∩ C = {3, 6}.

Déterminons B ∩ C. Il n'y a aucun élément commun. Donc B ∩ C = ∅.

Déterminons A ∪ C. A ∪ C = {1, 2, 3, 4, 6, 9, 12, 15, 18}.

Déterminons B ∪ C. B ∪ C = {1, 2, 3, 4, 5, 6, 10, 12, 15}.

Représentation par diagrammes de Venn

Les diagrammes de Venn illustrent les relations entre ensembles. On utilise des cercles ou des ovales. L'intersection est la zone commune. La réunion est la zone totale couverte.

On considère deux ensembles A et B.

Si A ⊂ B, le cercle représentant A est entièrement contenu dans le cercle représentant B.

Si A ∩ B = ∅, les cercles représentant A et B ne se chevauchent pas.

La zone de A qui n'est pas dans B représente A \ B (A moins B).

La zone de B qui n'est pas dans A représente B \ A (B moins A).

L'extérieur des cercles représente l'ensemble complémentaire par rapport à un ensemble universel défini.

Exercices avancés

Soit E l'ensemble des élèves de 4ème.

Soit F l'ensemble des élèves faisant du sport.

Soit G l'ensemble des élèves jouant d'un instrument de musique.

E ∩ F représente les élèves de 4ème faisant du sport.

E ∩ G représente les élèves de 4ème jouant d'un instrument de musique.

F ∩ G représente les élèves faisant du sport et jouant d'un instrument de musique.

E ∩ F ∩ G représente les élèves de 4ème faisant du sport et jouant d'un instrument de musique.

E ∪ F représente l'ensemble des élèves de 4ème ou faisant du sport (ou les deux).

E ∪ G représente l'ensemble des élèves de 4ème ou jouant d'un instrument de musique (ou les deux).

Utilisation des nombres premiers

Soit P l'ensemble des nombres premiers inférieurs à 30. P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}.

Soit A l'ensemble des diviseurs premiers de 60. A = {2, 3, 5}.

Déterminer A ⊂ P. Oui, A est inclus dans P.

Soit B l'ensemble des diviseurs premiers de 210. B = {2, 3, 5, 7}.

Déterminer B ⊂ P. Oui, B est inclus dans P.

Déterminer A ∩ B. A ∩ B = {2, 3, 5}.

Déterminer A ∪ B. A ∪ B = {2, 3, 5, 7}.

Conclusion

La classification en groupes emboîtés est fondamentale. Elle structure la pensée logique. Les exercices permettent de maîtriser les concepts. Les diagrammes de Venn visualisent les relations. La pratique régulière est essentielle.