Classification En Groupes Emboîtés Collège Exercices Corrigés

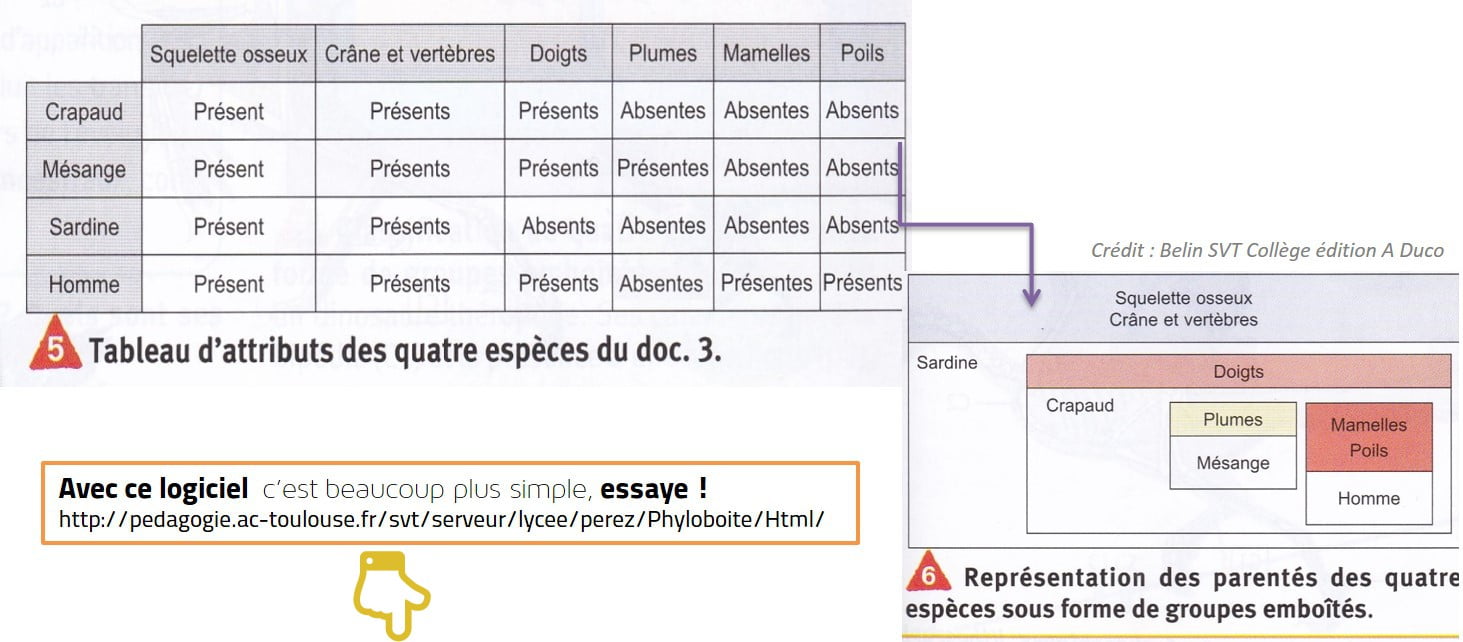
La classification en groupes emboîtés est une méthode hiérarchique ascendante. Elle permet de structurer des données en fonction de leur similarité. Au collège, cette méthode est abordée de manière simplifiée. L'objectif est d'initier les élèves aux concepts de classification et de regroupement.

On part d'un ensemble d'individus. Chaque individu forme initialement un groupe. On calcule ensuite la distance ou la dissimilarité entre chaque paire de groupes. Le choix de la distance est crucial. La distance euclidienne est souvent utilisée.

Les deux groupes les plus proches sont fusionnés. Cette fusion forme un nouveau groupe. On recalcule les distances entre ce nouveau groupe et les autres groupes restants. Ce processus est répété. Il l'est jusqu'à ce qu'il ne reste plus qu'un seul groupe contenant tous les individus.

La représentation visuelle de cette classification est un dendrogramme. L'axe horizontal du dendrogramme représente les individus ou les groupes. L'axe vertical représente la distance à laquelle les groupes ont été fusionnés. La hauteur des branches indique le niveau de dissimilarité.

L'interprétation du dendrogramme est essentielle. Elle permet de visualiser les regroupements. Elle permet de déterminer le nombre de groupes pertinents. Un seuil de distance est choisi. Les groupes formés en dessous de ce seuil sont considérés comme significatifs.

Exercices corrigés :

Exercice 1 :

Quatre animaux sont considérés : un chat, un chien, un poisson rouge et un canari. On définit les caractéristiques suivantes :

Le chat et le chien sont des mammifères.
Le poisson rouge est un poisson.
Le canari est un oiseau.

Solution :

Initialisation : Chaque animal forme un groupe. {Chat}, {Chien}, {Poisson Rouge}, {Canari}
Fusion 1 : Le chat et le chien sont regroupés car ils partagent la caractéristique "mammifère". {Chat, Chien}, {Poisson Rouge}, {Canari}
Pas de fusion supplémentaire évidente basée sur une seule caractéristique.

Le dendrogramme montrerait une fusion précoce du Chat et du Chien. Le Poisson Rouge et le Canari resteraient distincts plus longtemps.

Exercice 2 :

Trois villes sont considérées : Paris, Lyon et Marseille. On utilise la distance géographique en kilomètres comme mesure de dissimilarité. Les distances sont les suivantes :

Paris-Lyon : 470 km
Paris-Marseille : 775 km
Lyon-Marseille : 315 km

Solution :

Initialisation : {Paris}, {Lyon}, {Marseille}
Fusion 1 : Lyon et Marseille sont les plus proches (315 km). {Paris}, {Lyon, Marseille}
Fusion 2 : Paris est fusionnée avec le groupe {Lyon, Marseille}. {Paris, Lyon, Marseille}

Le dendrogramme montrerait une fusion de Lyon et Marseille à une faible hauteur (315 km). Paris rejoindrait ce groupe à une hauteur plus élevée (distance de Paris à ce nouveau groupe, qui dépendra de la méthode d'agrégation utilisée).

Exercice 3 :

Cinq élèves ont obtenu les notes suivantes à un contrôle : 10, 12, 14, 11, 13. Classer ces élèves en groupes en utilisant la similarité de leurs notes.

Solution :

Initialisation : {10}, {12}, {14}, {11}, {13}
On calcule les différences de notes entre chaque élève. Par exemple, |10-12| = 2, |10-14| = 4, etc.
Fusion 1 : 10 et 11 sont les plus proches (|10-11|=1). {10, 11}, {12}, {14}, {13}
Fusion 2 : 12 et 13 sont proches (|12-13|=1). {10, 11}, {12, 13}, {14}
Fusion 3 : 10 et 11 se rapprochent de 12 et 13. On calcule une distance du type "distance moyenne entre les groupes". Distance entre {10,11} et {12,13} = ((|10-12|+|10-13|+|11-12|+|11-13|)/4) = (2+3+1+2)/4 = 2. {10, 11, 12, 13}, {14}
Fusion 4 : 14 est fusionné avec le groupe restant. {10, 11, 12, 13, 14}

Exercice 4 :

Quels sont les avantages et les inconvénients de la classification en groupes emboîtés ?

Solution :

Avantages :

Simplicité de compréhension et d'application.
Permet de visualiser la structure des données.
Ne nécessite pas de définir le nombre de groupes à l'avance.

Inconvénients :

Sensible au choix de la mesure de distance.
Peut être coûteuse en calcul pour de grands ensembles de données.
Les décisions de fusion sont irréversibles.

Exercice 5 :

Décrire le rôle du dendrogramme dans la classification en groupes emboîtés.

Solution :

Le dendrogramme est une représentation graphique. Il visualise l'ensemble du processus de classification. Il représente les individus et les groupes. Il montre les distances de fusion. Il aide à identifier les regroupements significatifs. Il facilite l'interprétation des résultats.

L'utilisation de différents critères d'agrégation influence le résultat final. Les critères les plus courants sont :

Liaison simple (minimum de distance)
Liaison complète (maximum de distance)
Liaison moyenne (distance moyenne)
Centroïde
Ward

Chaque critère a ses propres caractéristiques et peut conduire à des regroupements différents. Le choix du critère dépend de la nature des données et de l'objectif de la classification.

L'interprétation correcte du dendrogramme nécessite une certaine expérience. Il est important de considérer le contexte des données. Il est important d'utiliser des connaissances préalables pour valider les regroupements. Un examen critique des résultats est indispensable.