Calculer Les Cotés D'un Triangle Rectangle Avec L'hypoténuse

Commençons par le cas le plus direct : vous connaissez l'hypoténuse et un autre côté. Notre objectif est de déterminer le côté manquant.

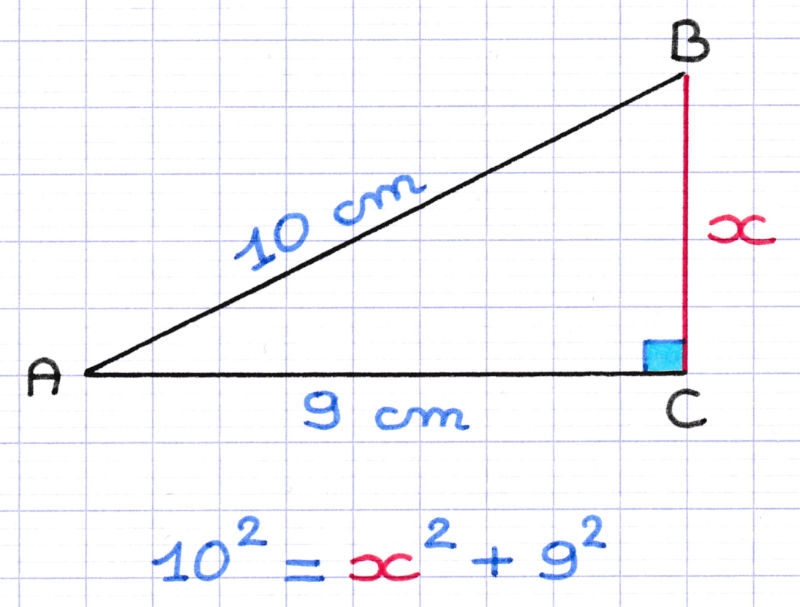
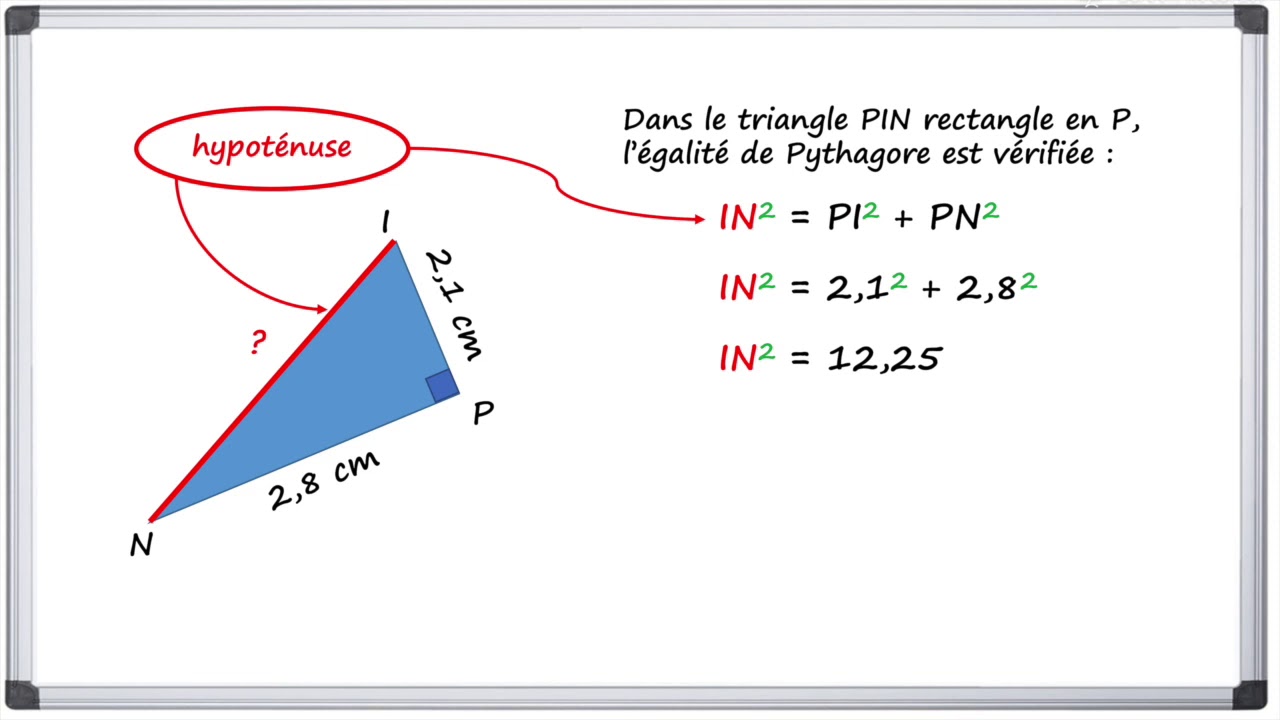
Appliquons le théorème de Pythagore : a² + b² = c², où 'c' est l'hypoténuse.

Réarrangeons l'équation pour isoler le côté que nous cherchons. Supposons que nous connaissions 'c' et 'a', et que nous voulions trouver 'b'.

Alors : b² = c² - a².

Extrayons la racine carrée des deux côtés : b = √(c² - a²).

Voilà ! Vous avez la longueur du côté manquant.

Exemple concret

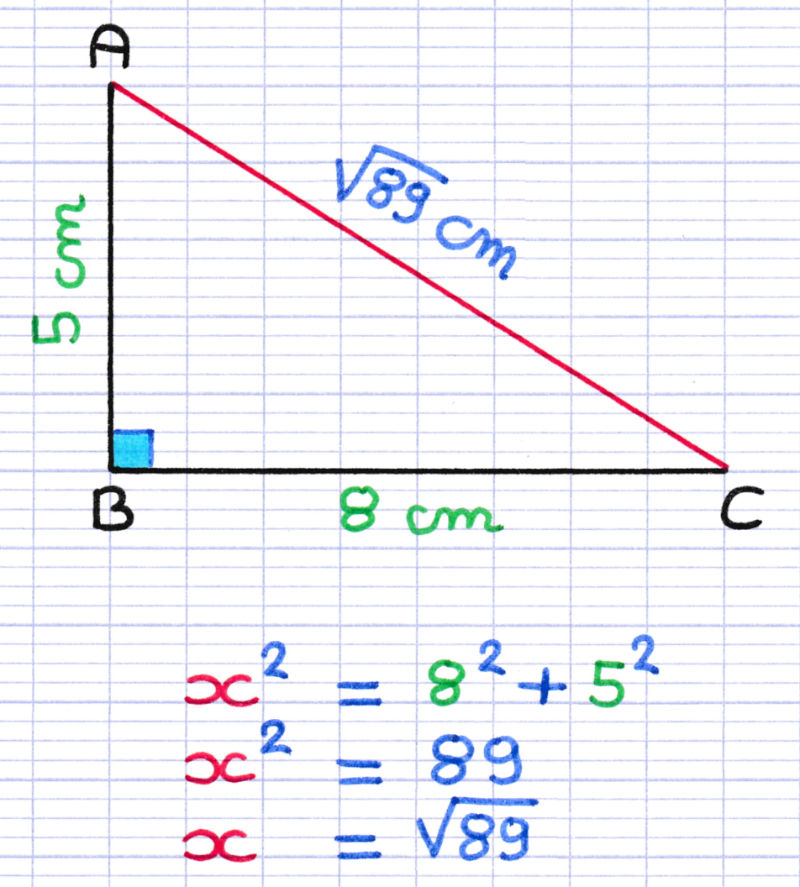
Imaginez un triangle rectangle avec une hypoténuse de 10 cm et un côté de 6 cm. Nous cherchons la longueur du troisième côté.

Appliquons la formule : b = √(10² - 6²).

Cela donne : b = √(100 - 36).

Donc : b = √64.

Finalement : b = 8 cm. Le côté manquant mesure 8 cm.

Que faire si on ne connaît que l'hypoténuse et un angle ?

C'est ici que la trigonométrie entre en jeu. Nous utilisons les fonctions sinus, cosinus et tangente.

Si vous connaissez l'angle opposé au côté que vous cherchez (appelons-le 'a'), utilisez le sinus.

sin(angle) = côté opposé / hypoténuse = a / c.

Donc, a = c * sin(angle).

Si vous connaissez l'angle adjacent au côté que vous cherchez (appelons-le 'b'), utilisez le cosinus.

cos(angle) = côté adjacent / hypoténuse = b / c.

Donc, b = c * cos(angle).

Illustration

Supposons un triangle rectangle avec une hypoténuse de 12 cm et un angle de 30 degrés opposé au côté 'a'.

Calculons 'a' : a = 12 * sin(30°).

Sachant que sin(30°) = 0.5, nous avons : a = 12 * 0.5 = 6 cm.

Calculons 'b' : b = 12 * cos(30°).

Sachant que cos(30°) ≈ 0.866, nous avons : b = 12 * 0.866 ≈ 10.39 cm.

Vérification

Pour vérifier nos calculs, on peut utiliser le théorème de Pythagore.

a² + b² = 6² + 10.39² ≈ 36 + 107.95 ≈ 143.95.

c² = 12² = 144.

Les valeurs sont très proches, compte tenu de l'arrondissement de cos(30°). Cela confirme la validité de nos calculs.

Astuces supplémentaires

N'oubliez pas que la somme des angles d'un triangle est toujours de 180 degrés. Dans un triangle rectangle, un angle est de 90 degrés. Donc, si vous connaissez un angle aigu (autre que l'angle droit), vous pouvez trouver l'autre en soustrayant cet angle et 90 de 180.

Angle manquant = 180 - 90 - angle connu.

Ensuite, vous pouvez utiliser cette information pour appliquer les fonctions trigonométriques décrites précédemment.

Assurez-vous que votre calculatrice est en mode "degrés" si vous travaillez avec des angles en degrés.

Portez une attention particulière aux unités de mesure. Si l'hypoténuse est en centimètres, les côtés seront également en centimètres.

Si les valeurs obtenues semblent irréalistes (par exemple, un côté plus long que l'hypoténuse), vérifiez vos calculs et la formule que vous avez utilisée. Une erreur de calcul est possible.

La précision des résultats dépend de la précision de vos mesures et des valeurs des fonctions trigonométriques que vous utilisez (nombre de chiffres après la virgule).

Cas particuliers

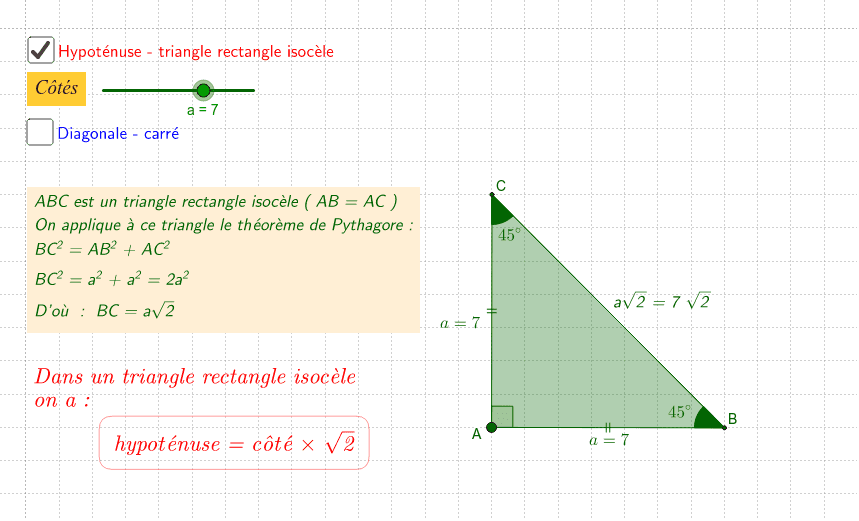
Si le triangle rectangle est également isocèle (deux côtés égaux), les angles aigus sont de 45 degrés. Le rapport entre l'hypoténuse et un côté est alors √2.

c = a√2 (où 'a' est la longueur d'un des côtés égaux).

Si vous connaissez 'a', vous pouvez calculer 'c' : c = a√2.

Si vous connaissez 'c', vous pouvez calculer 'a' : a = c / √2.

Conclusion

Déterminer les côtés d'un triangle rectangle à partir de l'hypoténuse est une application directe du théorème de Pythagore et de la trigonométrie. En comprenant ces principes fondamentaux et en appliquant les formules appropriées, vous pouvez résoudre n'importe quel problème de ce type. N'oubliez pas de vérifier vos calculs et de faire attention aux unités de mesure pour garantir l'exactitude de vos résultats. La pratique régulière renforce la maîtrise de ces concepts.