Calculer La Hauteur D'un Triangle équilatéral De Côté 5 Cm

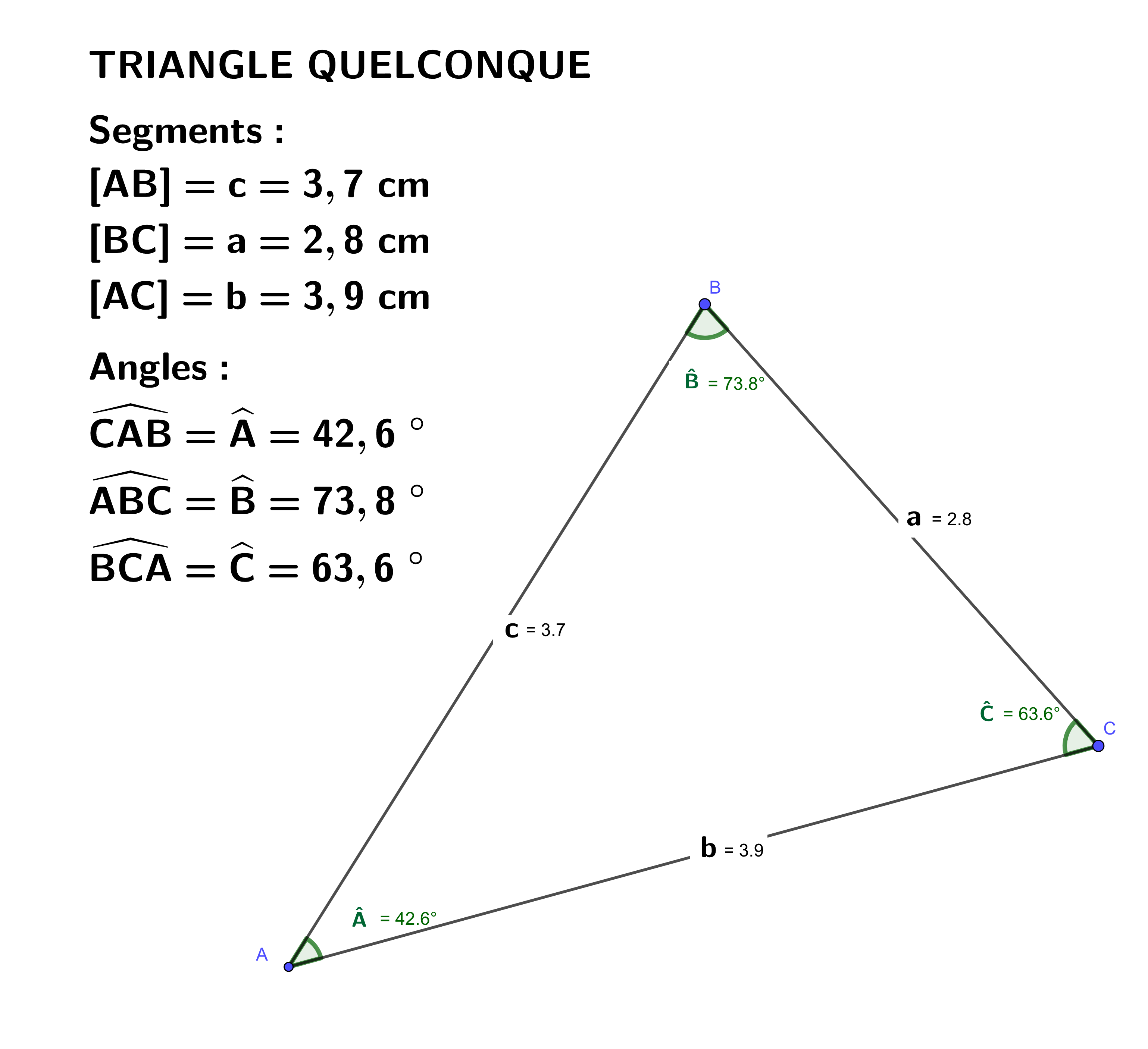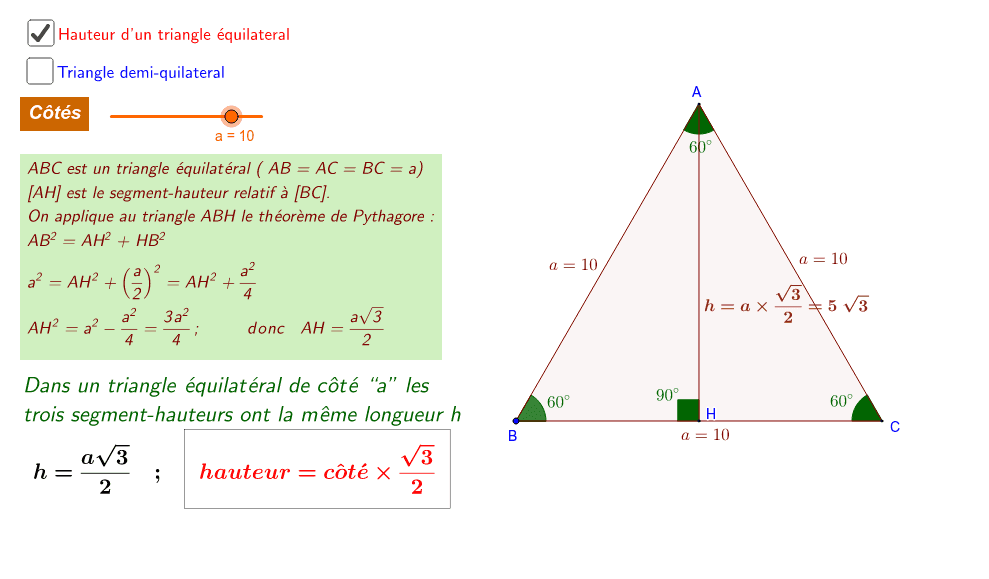
Un triangle équilatéral, par définition, possède trois côtés de même longueur. Ici, cette longueur est de 5 cm.

Pour déterminer la hauteur de ce triangle, nous allons recourir à une approche géométrique précise.

Méthode de Calcul

La hauteur d'un triangle équilatéral coupe la base en son milieu. Ceci forme deux triangles rectangles congruents. Chaque triangle rectangle a donc une base de 2.5 cm (la moitié de 5 cm), une hypoténuse de 5 cm (le côté du triangle équilatéral), et une hauteur que nous cherchons à calculer.

Appliquons le théorème de Pythagore : a² + b² = c²

Où :

c est la longueur de l'hypoténuse (5 cm)
a est la longueur de la moitié de la base (2.5 cm)
b est la hauteur du triangle équilatéral (ce que nous cherchons)

Alors : (2.5)² + b² = (5)²

Ce qui donne : 6.25 + b² = 25

Donc : b² = 25 - 6.25 = 18.75

Et finalement : b = √18.75

En effectuant le calcul, nous obtenons : b ≈ 4.33 cm

La hauteur du triangle équilatéral de côté 5 cm est donc approximativement 4.33 cm.

Calcul de l'Aire

L'aire d'un triangle se calcule comme suit : (base x hauteur) / 2

Ici, la base est de 5 cm et la hauteur est d'environ 4.33 cm.

Aire = (5 cm x 4.33 cm) / 2

Aire = 21.65 cm² / 2

Aire ≈ 10.83 cm²

L'aire du triangle équilatéral est donc approximativement 10.83 cm².

Formule Générale

De manière générale, la hauteur d'un triangle équilatéral de côté a est donnée par la formule suivante:

hauteur = (a√3) / 2

Dans notre cas, avec a = 5 cm :

hauteur = (5√3) / 2

hauteur ≈ (5 x 1.732) / 2

hauteur ≈ 8.66 / 2

hauteur ≈ 4.33 cm

Nous retrouvons ainsi le même résultat. Cette formule est directement dérivée du théorème de Pythagore appliqué au demi-triangle rectangle formé par la hauteur.

Vérification et Précision

Le calcul de la racine carrée (√18.75) et la valeur de √3 sont souvent arrondies. Plus la précision des valeurs utilisées est grande, plus le résultat final le sera également. L'utilisation d'une calculatrice scientifique ou d'un logiciel de calcul permet d'obtenir une précision maximale.

L'approximation à deux décimales (4.33 cm) est généralement suffisante pour la plupart des applications pratiques. Cependant, pour des calculs d'ingénierie ou de géométrie nécessitant une grande exactitude, il est préférable de conserver la forme exacte (5√3)/2 ou d'utiliser un nombre de décimales plus important.

La méthode décrite est valable pour tout triangle équilatéral, quelle que soit la longueur de son côté. Il suffit de substituer la valeur appropriée dans les formules. Il est crucial de se souvenir que cette méthode n'est applicable qu'aux triangles équilatéraux. Pour les autres types de triangles (isocèles, scalènes), des méthodes différentes doivent être employées.

Applications Pratiques

La connaissance de la hauteur d'un triangle équilatéral est utile dans de nombreux domaines :

Construction : Calculer la surface de toits triangulaires ou de structures architecturales.
Design : Créer des motifs géométriques précis.
Mathématiques et Physique : Résoudre des problèmes de trigonométrie et de mécanique.
Art et Artisanat : Concevoir des objets décoratifs ou des bijoux.

Bien que le calcul semble simple, sa maîtrise permet de résoudre des problèmes plus complexes impliquant des formes géométriques.

La compréhension des principes fondamentaux de la géométrie, tels que le théorème de Pythagore, est essentielle pour résoudre ce type de problème. La capacité à visualiser les relations spatiales et à appliquer les formules appropriées est également cruciale.